模式识别是一种应用范围很广的问题研究方法。它有一个分支，称为统计模式识别，即基于统计学，如平均值、方差等统计量，将不同的对象分到不同的类属中，达到分类的目的。在该分支中，有一种被普遍使用且很直观、易理解的方法：K最近邻（K Nearest Neighbor，KNN）。其原理如下：

设在空间中，已经存在一些已知分类的样本点，如图6.5.2中的小正方形和小三角形，因为这是一个两类问题，所以可将其类别值分别定义为+1和-1。现在有一未知样本点，见图6.5.2中的小圆点，问它应该属于哪一类？

KNN的求解步骤为：计算未知样本与所有已知样本的距离，并将其从小到大的顺序排列，挑选其中最小的K个，让这K个样本对新样本进行投票表决：

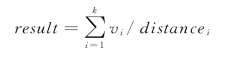
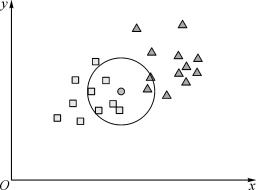
图6.5.2　KNN原理图

上式中，distancei代表新样本与挑选出来的第i个样本之间的距离，如果样本i属于第一类，则vi=1，否则vi=-1；

如果result＞0，则新样本归为第一类，否则归为第二类。

KNN算法非常简单，其依据的原理，仍然是统计模式识别的基本概念，那就是物以类聚。离未知样本最近的样本，是对未知样本最了解的，所以投票权值就大。

从图6.5.2中可以看出，在距离未知样本（圆点）最近的7个样本中，第一类有5个样本（方框），第二类有2个样本（三角）对未知样本进行投票，投票的结果决定未知样本属于第一类。

KNN算法的原理解释完毕后，在实现算法之前，先对问题域中的类进行分析如下：

（1）首先，空间中的每个点属于一类对象。设我们是在n维实数域中求解该问题，则每个点的坐标由n个实数组成，这是“点”类对象的属性。同时为实现模式分类，“点”类还有一个属性，就是其类别。对已知样本而言，它是已知的，对未知样本而言，它是待求解的属性。根据问题域的定义，“点”还有一个行为，计算它与其他点的距离。

（2）空间中的n个点，可以使用序列对象，序列中的每个元素就是一个“点”类对象。

（3）因为需要对求得的n个距离从小到大排序，且不能搞乱样本编号，因为投票表决时除了距离，还需要样本的分类值，即距离和样本的分类值是绑定在一起的。而通过为“点”对象再设定一个距离属性，就可将此问题解决好。(www.daowen.com)

故此，先将类定义如下：

Point类中，每个点的坐标用一个列表coordinate表示。

设已知空间中的8个点分成两类（菱形1，方框-1），及未知分类的一个点（三角型），如图6.5.3所示。

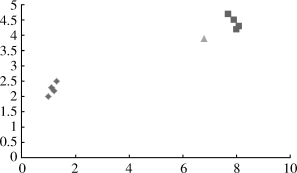
图6.5.3　已知分类的8个点及未知点在空间的分布

现在，在Point类的支持下，KNN算法判别未知点的分类程序如下：

程序的运行结果为：

-1

1

上例主要是让学习者了解，对于给定的问题，如何根据求解要求（求解域）对类进行分析，通过抽象，将问题求解方法归纳到类中，利用对象形成的列表，并充分利用列表带来的优势，编写出符合人类行为理解方式的程序。