科学研究中经常遇到一些用试验和理论思维难以解决的复杂问题，这其中有部分问题可以通过计算机模拟大大加快理论验证。例如材料领域晶体的随机生长、航天器飞行的空气动力学计算、核反应体系中子碰撞过程，等等。这类问题求解中的模拟手段也是计算思维的体现。

图1.2.3是利用计算机模拟得到的多晶材料晶粒生长情况，可为材料研究提供新的方法和重要依据。

下面我们以一个简单的求解f（x）=e-x函数在区间[0，1]的积分为例，来谈谈随机模拟求解的实现方式。虽然该例用高等数学的理论很容易求解，但这里我们采用一种完全不同的思路求解，以扩展读者计算求解的思路。

先观察一下图1.2.4，图中曲线即为f（x）=e-x。如果将此图看作一幅数字化的图片，则可以将积分看作是曲线下面的点占总点数的百分比。

图1.2.3　多晶材料晶粒生长的计算机模拟

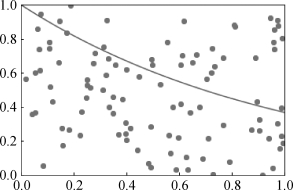
图1.2.4　计算机模拟求解定积分

这是一个特殊设计的例子，函数及自变量所在的区间都在[0，1]范围内，这个矩形的面积为1，因而曲线下面的面积（积分），正好是曲线下面的所有点占矩形全部点的百分比。

为使问题可模拟求解，可设定如下的随机过程：不断在矩形（0≤x≤1，0≤y≤1）中产生均匀分布的点，这产生了两个服从[0，1]均匀分布的随机量X、Y，且两者相互独立。定义事件

A={Y≤f（x）}，然后计算A事件发生的概率，当在图1.2.4中随机产生大量的点时，A事件的概率就接近真值，此时，A的概率就是问题的近似解。

故此，设计如下的求解伪码：

设定产生的所有的点数N

产生N个随机小数，记录到X（x1，x2，…，xn）中

再产生N个随机小数，记录到Y（y1，y2，…，yn）中(www.daowen.com)

曲线下面的点数count初值=0

令i从1到N循环

根据xi，计算函数值f（x）=e-xi

如果f（x）≤yi，则count=count+1

计算概率count/N

对应的Python程序如下：

程序：模拟求积分

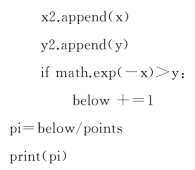
以下是用Python编写的程序在不同N值时的计算结果，见表1.2.1：

表1.2.1　蒙特卡洛模拟计算定积分

从计算结果可以看到，随着随机点数的增加，结果逐步逼近真值。