高等数学中求解函数积分时，通过将积分区间分割成无限小的梯形来求解，如图1.2.1所示：

在梯形无限小时，所有小梯形的面积之和，就是函数在区间[a，b]中的积分。在用计算机求解该类问题时，摆在我们面前的一个问题是：小梯形区间小到什么时候才算无限小？因为用计算机计算时，不可能像高等数学理论中讲的那样无限小。如果这样，这个问题就算不完了。那如何使这样的问题变得可编程计算？此时可以利用容错概念，即将梯形的无限小定义为当梯形小到一定程度，再小下去时，求得的积分变化几乎可以忽略不计。此时，虽然求得的积分值不是精确解，但对计算求解而言，已经可以满足要求的精度。

在这样的指导原则下，梯形求解积分就变得可计算。由此，可以设计这样的思路：

先将积分区间分成n份，求得一个积分值S1。

将积分区间份数扩大为原来的两倍，即2n份，再求一个积分值S2。

如果S1-S2的绝对值足够小，则求解过程结束，否则再将区间分成4n份，如此反复增加积分区间的份数，达到求解的目的。

上述思考得到的求解方法，由于事先难以得知划分小区间的最佳份数，所以，需要一个自动化的循环迭代过程来求解。通过循环，不断将原来的小区间份数变成原来的2倍，并比较前后2次所求积分的差值。因此使用循环的求解过程可以描述如下：

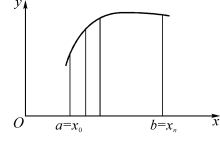
图1.2.1　梯形法求积分

将区间看作一个大梯形，区间计算面积记录到T2，小区间个数n=1

令精度为eps=10-6(www.daowen.com)

循环开始

令T1=T2

令n=2n

计算新的面积T2

如果T1-T2的绝对值小于eps，计算结束

否则转到循环开始位置

这种循环迭代配合精度的策略，在计算求解的过程中经常使用。例如求解e-x的近似值，sin（x）的近似值等问题，将它们用级数展开后，可以分别得到如下的公式：

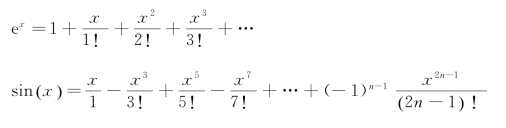
该类问题，通过分析其计算公式，在给定精度的条件下，都可以通过循环的方式实现求解。