【知识链接】

数字电子计算机在信息处理和存储时都采用二进制。计算机中的数值与非数值信息都是由0和1组成的二进制代码，经常使用以下两种单位。

（1）位（bit）。位是度量数据的最小单位，在计算机中无论是0还是1都是占用1位。

（2）字节（Byte。字节是信息处理和存储的基本单位，也是计算机体系结构的基本单位。1个字节由八位二进制数字组成（1Byte=8bit）。

一、数制

人们在日常生活和生产实践中创造了许多表示数的方法，这些数的表示规则称为数制。学习数制及其转换方法前，我们先了解数码、基数、位权和数制符号等基本知识，如表1-4所示。

表1-4　数制

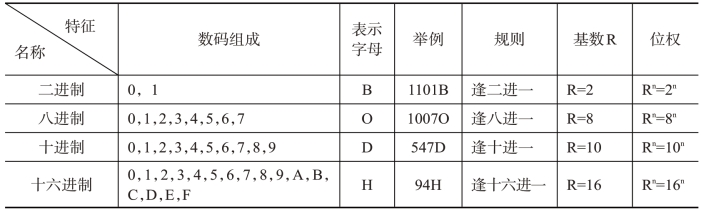
说明：

（1）数码：指数制中表示不同值的基本数字符号。

（2）基数：指数制中可使用的数码个数。例如，二进制的基数是2，十进制的基数是10。

（3）位权：数制中某一位置上的1所表示数值的大小。例如，十进制数56，十位上的5的位权是10（即101）。

二、数制的转换

1.将二进制转换成十进制

把二进制转换成十进制数用“按位权相加”法，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

例：将二进制1101转换为十进制数：（1101）2=（　）10

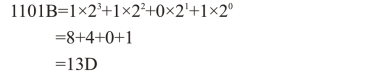
2.将十进制数转换为二进制数（采用“除2取余”法）

例：将十进制数26转换为二进制数：26D=（　）B

3.二进制、八进制和十六进制的相互转换

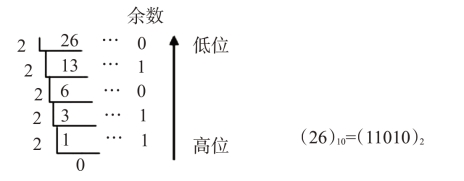
（1）八进制转换成二进制。

方法：每一位八进制数拆成三位二进制数。

例：（453）8=（　）2

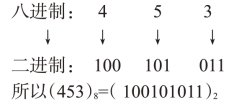
（2）二进制数转换成八进制。

方法：整数从右到左每三位二进制数合成一位八进制数，当不足三位时，在前面加0补足。

例：将二进制数1100100101转换成八进制数。

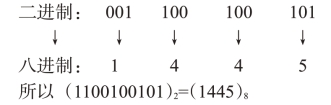
（3）将十六进制转换成二进制。

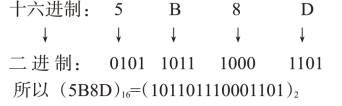
方法：将一位十六进制数拆成四位二进制数。

例：将十六进制数5B8D转换成二进制数。

（4）将二进制数转换成十六进制数。

方法：整数从右到左每四位二进制数合并成一位十六进制数，不足四位在前面用0补足。

例：将二进制数1101001110转换成十六进制数。

【课堂练习】

1.5位无符号二进制数字最大能表示的十进制整数是（　）。

A.64

B.63

C.32

D.31

2.将二进制数10000001转换为十进制数应该是（　）。(www.daowen.com)

A.127

B.129

C.126

D.128

3.下列4个二进制数中，（　）与十进制数510等值。

A.111111111B

B.100000000B

C.111111110B

D.110011001B

4.下列不同进制的4个数中，最大的一个数是（　）。

A.1010011B

B.257O

C.689D

D.1FFH

5.二进制数011111转换为十进制整数是（　）。

A.64

B.63

C.32

D.31

6.用7个二进制位能表示的最大的无符号整数等于十进制整数（　）。

A.127

B.128

C.255

D.256

7.在一个非零无符号二进制整数之后添加一个0，则此数的值为原数的（　）倍。

A.4

B.2

C.1/2

D.1/4

8.十进制数121转换成二进制数是（　）。

A.1111001

B.111001

C.1001111

D.100111

9.在数制的转换中，下列叙述中正确的一条是（　）。

A.对于相同的十进制正整数，随着基数R的增大，转换结果的位数小于或等于原数据的位数

B.对于相同的十进制正整数，随着基数R的增大，转换结果的位数大于或等于原数据的位数

C.不同数制的数字符是各不相同的，没有一个数字符是一样的

D.对于同一个整数值的二进制数表示的位数一定大于十进制数字符的位数

10.一个字长为8位的无符号二进制整数能表示的十进制数值范围是（　）。

A.0～256

B.0～255

C.1～256

D.1～255