角动量守恒是推演宇宙演化的一个重要依据。根据现行理论，天体即使坍缩为黑洞，黑洞中的角动量仍然守恒。如果在产生当前宇宙的原始火球中存在角动量，则现在的宇宙也应该存在角动量；反之则没有。如果公式(15-1)和公式(15-3)正确，那我们就可以得到“宇宙大爆炸模型中的角动量为零”的结论。也存在特殊情况，与(15-1)式中的径向速度相比，当天体相对于宇宙中心的角速度很小，或与天体的径向动量相比，天体的角动量很小时，就意味着我们现在宇宙中的星系存在围绕宇宙中心的角动量，只是目前没有发现。由于角动量只能依靠观测天体的自行或光行差才能发现，并且天体与我们的距离越远，自行越难发现，大距离天体的自行一般需要几千年，甚至上万年才能发现。我们现在的宇宙是否存在角动量目前不能得出结论。

在图16-2中，若有一星系P在宇宙年龄的某时刻t到大爆炸中心O点的距离为r，AB两星系在同一时刻到O点的距离分别为r1、r2。根据(15-1)式，星系P及星系AB分别与大爆炸中心O点的相对速度为

星系A，B，P之间的相对速度分别为

以上三式可以组成两个三角形：ΔvPAvPBvAB和Δ(r1-r)(r2-r)(r2-r1)。由于是同一宇宙年龄的数据，并且假设r1、r2、r的大小差别不大，因此满足前面分析的哈勃公式成立条件。根据哈勃公式，H是常数，因此这两个三角形相似。

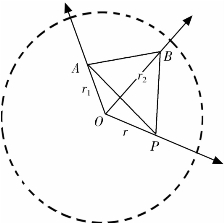
图16-2(www.daowen.com)

假设，经过时间Δt，三星系相对于O点的速度增加值分别为Δv1，Δv2和ΔvP，由此造成的三星系的距离增加值分别为ΔdA，ΔdB和ΔdP，相对速度的增加值分别为ΔVAB、ΔVBP、ΔVPA。同样满足哈勃公式成立条件，则后面两个增量三角形是相似三角形，并且与(15-3)式、(15-4)式和(15-5)式组成的三角形相似。我们还可以得到以下方程

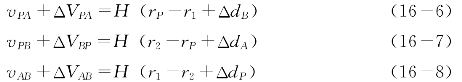
根据哈勃公式，(16-6)式、(16-7)式和(16-8)式中的距离组成的Δ(rP-r1+ΔdB)(r2-rP+ΔdA)(r1-r2+ΔdP)和(16-3)式、(16-4)式和(16-5)式中的距离组成的Δ(r1-r)(r2-r)(r2-r1)相似。根据宇宙学定理，P、A、B都是欧氏空间中的星系，因此以上两个三角形都是欧氏空间中的相似三角形，两个三角形的对应角相等。这说明，任意两个星系之间的距离对第三个星系所张的视角与时间无关。换言之，若以宇宙中任意一个天体为参照系，则在该天体上，将观察到星空(宇宙)中所有星系在天球上的视位置是固定的，即星系的天象是固定的。

这一结论为宇宙学原理提供了解释。在天球上同一天区中，我们虽然看到的是不同宇宙年龄天象的组合，但其天象与同一宇宙年龄的天象是相同的。这是在宇宙的角动量为零的前提下得到的。如果经过长期观察，观察期可能需要几千年以上，发现星系在天球位置上移动，有自行现象，即星空中星系的天象不是固定的，说明宇宙的角动量不为零，即星系存在围绕宇宙中心转动的运动。即使宇宙的角动量为零，“天象是固定的”结论也仅限于线度大于或等于星系的天体，在同一星系内这一结论显然不正确。因为在同一星系内的天体相对于星系中心都存在转动，它们相对于星系中心的角动量都不为零，这是已经为天文观测证实了的事实。

星系内的天象不是固定的，应该是怎样的呢?星系内的天象应该是循环的。理由是，同一星系内的所有天体都在以不同周期围绕星系中心转动。相对于同一星系内某些确定的天体而言，这些天体的旋转周期必然存在最小公倍数，因此在每一个最小公倍数周期内，这些天体的对应位置必然循环一次。

若干年前我国的《科学画报》上有一则报道，标题是“七千年前的天文学家”。里面讲某科学家在欧洲一处山洞中发现由七个点组成的石刻，很像北斗七星。科学家经过计算，认为该石刻就是大约七千年前地球上看见的北斗七星。很明显，在北斗七星围绕银河系中心旋转周期的最小公倍数周期内，北斗七星之间的相应位置将循环一次，即地球上看见的北斗七星的图像将重复再现一次。

根据星系内天体普遍存在围绕星系中心运动的现象分析，宇宙演化过程中应该存在围绕宇宙中心运动的角动量。其物理意义是，遥远的星系与我们之间存在和退行速度垂直的横向速度，或者说遥远的星系在天球背景上存在自行现象。反之，遥远的星系是否存在自行，也是检验宇宙演化过程中，是否存在围绕宇宙中心运动的角动量的唯一方法。只是，这个过程可能至少需要上千年。