如果在引力场中心天体表面附近任意AB两点，发射一条光线将两点连接起来，则根据直线的定义，AB是引力场空间中的一条直线。在AB两点所在的同一平面，各发射一条光线与直线AB垂直(如图13-1所示)。

根据欧几里得几何，在同一平面内，直线DD′、CC′垂直于同一直线AB，AD、BC是平行线。由于在引力场空间的平直性的意义不同，从图13-1可以看出，直线DD′、CC′虽然垂直于同一直线，却可能在有限的距离内相交，至少在无限远处必然相交。它说明，在引力场空间的任意平面内，过直线外一点不能作一条直线与已知直线平行，这就是黎曼几何第五公设的一种表述形式。在图13-1中，如果假设直线AD、BC相交于C点(如图13-2所示)，根据已知，由于AC、BC都垂直于AB，因此∠A+∠B=180°，因此∠A+∠B+∠C＞180°。在本质上，由于引力场中的直线是两头向引力场方向弯曲，中间向引力小的方向凸出，因此三角形ABC的内角和大于180°。在这个例子中，如果引力场非常强，直线AB、BC、CA可以弯曲(按欧氏空间的观点)得更厉害，∠C的值可以接近180°，三角形内角和可以接近360°。引力场中三角形内角和大于180°，小于360°，这就是黎曼几何第五公设的另一种表述形式。因此引力场空间的任意平面满足黎曼几何的第五公设，引力场空间是黎曼几何对应的自然空间。引力场空间的任意平面满足黎曼几何的第五公设说明：将引力场空间的光线轨迹定义为直线正确。

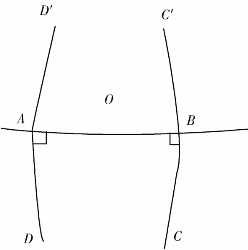
图13-1

(www.daowen.com)

图13-2

如果引力场空间中的平面面积越小或离中心天体越远，其性质越接近欧氏平面；平面如果可以与天体越近，其面积可以与天体的截面积比较，其黎曼平面的性质越显著。

在黎曼几何中，有一个表征黎曼平面空间性质内禀性的常数，这个常数越大，黎曼平面的空间性质越接近欧氏平面；越小，其黎曼空间性质越显著。上述分析说明，表征黎曼平面内禀性的常数实际就是平面到引力中心的距离R。上述分析还说明，黎曼几何分析讨论的不是整个引力场空间，而是将引力场空间的所有平面分割为无限多个R近似不变的二维子空间，事实上罗巴切夫斯基几何与此也类似。

以上的分析说明，在引力场空间中的观察者看来，引力场空间的性质与欧氏空间完全相同，空间同样是平直的。仅是空间中任意平面的性质稍有不同，欧氏平面满足欧氏几何的第五公设，引力场平面满足黎曼几何的第五公设。第五公设不同，说明空间的内禀性不同；其他性质相同，说明空间的外延性相同。这也说明黎曼几何与物理的引力场空间对应。引力场空间的本质是欧氏空间和引力场叠加而成的空间。