根据牛顿力学，物体的质量与运动无关，也与引力场无关。光子在引力场与欧氏空间中的质量相同，都是由于引力场中心天体的电磁辐射会造成天体的质量损失，引力场的强度一般会随着时间的流逝而变小。

例：地球对太阳辐射的吸收率为1.34×103W/m2，求太阳由于辐射引起的质量损失率。太阳质量现在约为2.0×1030kg。

解：假定太阳的辐射各向同性，则太阳的总辐射率为单位时间内通过一个以地球与太阳平均距离1.49×1011m为半径r的球面辐射。

因为

所以

太阳每秒损失约8.72百万吨质量，太阳质量在一年的损失率为

如果太阳一直按照现在辐射的规模不变，将在万亿年燃烧殆尽。地球绕日公转的速度为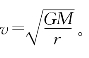太阳的质量因辐射而减小，地球绕日公转的速度也会随着时间的推移而减小，即一年的时间会逐渐变长。另一方面，地球自转会因为潮汐作用而变慢。这说明由“世界时”确定的年、月、日、秒都是不准确的。同样理由，双星系统也会由于辐射而损失轨道能量，使旋转速度变小。光子具有质量，恒星由于辐射产生质量损失是必然结果。虽然辐射引起的质量的相对损失率很小，但是时间的积累会使这一效应显著。

在引力场中光子吸收引力能使能量增加，能量增加的形式是速度增加，由欧氏空间中的c增加为引力场中的C。根据(11-4)式，光子在引力场中任意一点R处的动能为

设光子在欧氏空间的能量为 可以求出(www.daowen.com)

前面已经说明，对一般恒星而言，β的值和1的差别很小，对一般恒星而言E和E0的差别也很小。

设光子在引力场中的能量增加值为ΔE=E-E0，根据(12-6)式有

在黑洞表面光子能量增加1倍。若光子从引力场中的R1运行至R2，能量的改变量为

在相同情况下，光速或光子速度改变量为

在相同情况下，光的波长改变量为

式中λ0为单色光在欧氏空间中光源与引力中心天体相对静止时的波长。

上述分析说明在引力场中，光子速度将随着引力场相对强度的改变而改变，光子满足能量守恒定律，并且光子数量也守恒。

以上对光子能量的分析还说明，光子在引力场中任意一点R处的能量，是一个仅与R位置有关的位置函数，与光子从哪里来到哪里去无关，与光子的路径无关。可以将(12-8)式ΔE称作引力场在P(R)点的位能；(12-9)式ΔE′称作R1与R2两点的位能差。