1919年5月29日，英国天体物理学家爱丁顿领导的观测队，在非洲西部的普林西比岛拍摄了日全食时太阳附近的星空照片，第一次定量地证实了广义相对论关于光线弯曲的预言，爱因斯坦按照空间弯曲的观点解释了这一现象。

另一方面，如果将光看作粒子(光子)，根据动力学理论，光线弯曲现象可以认为是光子在引力场中的速度发生了改变。这一观点可以得到什么结论，是否和实验吻合呢?下面按照这一思路讨论光子在引力场中的速度变化。

设有一束光从无限远的欧氏空间的P点，射向质量为M、半径为r的天体O产生的引力场空间，初始方向为PB，在引力作用下光线向引力场中心方向弯曲。在到达该天体表面的某点A时，光子的速度在M的引力作用下由c增加为C，并且与天体表面相切。根据万有引力定律，引力对光子从P到A所作的功为

其中，μ=2h/c2，为光子的质量，h为约化普朗克常数。

如图11-1，设光线从无限远处的P点射向天体O。如果没有天体O的引力，光线将一直沿着直线PB方向运动，现在由于天体的引力，光线的实际方向是沿着曲线PA前进，并且在A处与天体的表面相切。OA=r是天体O的半径。过A点做直线AB⊥PB交PB于B，过A点做⊙O的切线AD交PB于D。

在Rt△ABD中，若DB表示光线在原来欧氏空间中的光速c，即DB=c。BA表示光线在天体引力作用下速度的改变量v，即BA=v，则DA就是光线在A处的速度及方向，即DA=C。Rt△ABD就是光子的速度矢量三角形，光线到达A点时方向的改变量为α=∠ADB。另一方面，根据牛顿力学的动能公式，光子原来的能量为光子增加的能量为=BA。根据第五章光子的能量的分析，有△ABD既是

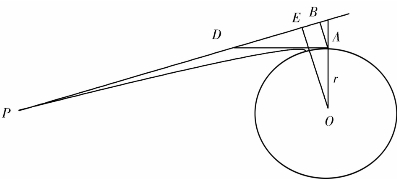
图11-1

光子的速度三角形，又是能量三角形，因此有

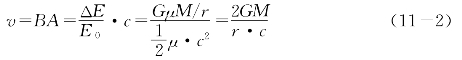
(11-2)式代入

根据(5-24)式，光子在天体表面A处的能量为

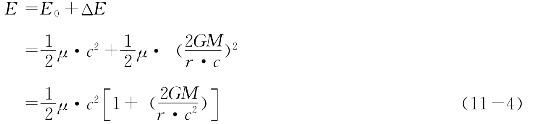
因为

所以

(11-5)式就是光子在天体表面的速度公式。(www.daowen.com)

在Rt△ABD中，知道了DB、BA和DA的值，就可以求出∠ADB的值

所以

或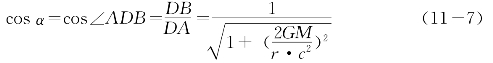

(11-6)式与广义相对论的表达式表面上完全相同，实际不同。(11-6)式中的是正切值，相对论中的是弧度值。当的绝对值很小时，的正弦、正切、弧度表示的角度都相同。如果的值越大，其正弦、正切、弧度表示的角度的差异越大。其中，正切表示的角度最小，弧度表示的次之，正弦表示的角度最大。例如，若=1，正切表示的角度为45°，弧度表示的角度约57°，正弦表示的角度为90°。(11-6)式与广义相对论的表达式在内涵上有差别。

光线在引力场中弯曲是对称的，如果考虑到光线离开引力场时产生的弯曲，则弯曲的角度是(11-6)式的两倍，即

代入太阳有关数据，有2α=1.75″。这个结果与日全食时星光掠过太阳表面观察到的弯曲结果是一致的。

如果将天体表面的点R理解为引力空间中的任意一点，根据(11-5)式，引力场中任意一点R的光子速度为

从无限远处的欧氏空间到该点，光线被引力场弯曲的角度为

分析结果证明了三点结论。

(1)光子是有质量的。

(2)光子是物质的运动形态，光子的能量是动能。

(3)光子质量与动能E的关系为

在《粒子与宇宙》一书中说：“广义相对论预测了引力作用引起的光的弯曲。基于牛顿观点的旧的引力理论也预测了这种现象，但广义相对论预测光弯曲的程度要比旧理论的预测大出两倍，这是由时空的弯曲造成的。大质量天体会扭曲它们周围的空间，包括光束在内的所有物体的轨道都被弯曲了。这个效应已经通过多种方法得到了证实，其中一种方法是测量星体发出的光经过太阳附近时星体位置的改变。太阳的存在使得星体发出的光发生偏转，从而我们观察到星体位置的改变。得到的结果和广义相对论非常吻合。”

这一段引文，抬高了广义相对论，贬低了牛顿经典理论。从(11-6)式可以看出，经典理论得到的光线在引力场中的弯曲结果与广义相对论完全相同。引文称“广义相对论预测光弯曲的程度要比旧理论的预测大出两倍”，是由于相对论计算光子在引力场中的弯曲时，光子质量是根据相对论的质能公式E=mc2得到的，本文的光子质量根据牛顿力学的动能公式得到。由牛顿力学得到的光子质量是相对论光子质量的2倍。根据经典理论得到的结果(11-6)式完全与广义相对论的结果相同，不存在“广义相对论预测光弯曲的程度要比旧理论的预测大出两倍”，这也说明牛顿的经典理论是正确的。

上述光子在引力场中的运动的讨论结果说明，相对于欧氏空间而言，光线在引力场中是弯曲的。弯曲的原因完全是由于光子受到引力作用，其速率和方向发生了改变，不存在空间弯曲。