天球坐标系事实上只能表征天体在天球上的位置，不能表征天体在天球坐标系中的运动。只有已经知道宇宙中所有天体与我们的相对距离时，天球坐标系才能表征天体相对于我们的运动，也才能表征所有天体之间的相对运动。这一工作经过近现代天文工作者的不懈努力，已臻于完善。

天文单位：太阳到地球之间的平均距离，英文缩写为AU。

光年：光在一回归年内通过的路程长度，英文缩写为l·y。

秒差距：一天文单位的张角为一角秒的角度时确定的距离，英文缩写为pc，因此有：

因此：

计量天体与地球(太阳)的距离，一般有以下方法。

1.视差法

又称三角形法。就是利用地球绕太阳运动的轨道直径观测被测恒星对该直径所张的角，然后根据该角确定恒星和太阳之间距离的方法(如图7-3所示)。

若某恒星对2AU所张的角为2θ，θ可以根据该恒星在天球上的位置的周年变化求出，有

(www.daowen.com)

则L即恒星与地球(太阳)的距离。

2.光度测距法

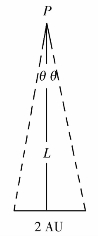
图7-3

天文学中常用绝对星等M来表征天体的实际光度，用视星等m表征观测到的亮度，二者的关系式为m-M=5lgr-5。m是观测量，只要设法确定恒星的M，便可以导出它的距离r，这就是光度测距法的基本原理，所得出的距离称为光度距离。该方法主要包含造父变星法、最亮恒星法、超新星法等，其中有代表性的是造父变星法。造父变星是一类周期性膨胀和收缩的超巨星，其发光强度(光度)有非常准确的周期关系。如果在某一星系或星系团中发现造父变星，可以根据该造父变星的周(期)光(度)关系，对某一时刻观测到的实际光度与该时刻的理论光度进行比较，得到该造父变星与我们的距离，由此确定该造父变星所在星系或星系团与我们的大概距离。天文学中又将造父变星称作“量天尺”。

当目标星系距离我们非常远时，已经不能辨认其中的造父变星，造父变星法就失效了，这时可以用“超新星法”。在现代天文观测中一般利用“Ia型超新星”测距。由于每颗“Ia型超新星”爆发时质量都一样，所以称为宇宙的“标准烛光”，测量到某一标准烛光的视亮度，就可以知道它相对于我们的距离。

3.哈勃原理法

通过多年观察，哈勃1929年总结出宇宙中星系都在互相背离，宇宙在膨胀，其背离速度v称作“退行速度”，v和星系之间的距离R成正比例关系。这一结论称作哈勃原理。根据哈勃原理有公式v=HR。其中H称作哈勃常数，R是星系与太阳的距离。根据观测确定H的值约为H≈50～100km/(s·Mpc)。即与太阳相距106pc(Mpc，约3×106光年)星系的退行速度为50～100km/s。根据哈勃原理和某一星系相对于我们的退行速度(退行速度由多普勒红移确定)，可以确定该星系与我们的大概距离。

以上三种方法，视差法最精确，测量的距离也最小，一般小于10000pc；亮度距离法介于二者之间，其测距的适用范围最远可达5000万光年，现在用Ia型超新星观测可以确定更远的距离；哈勃原理法测量的距离最远，精度最差。另外，还有一些特殊天体，可以用一些特殊的方法测距，具体方法从略。

掌握了天体与我们的距离和在天球上的位置，就可以利用天球坐标系计量天体相对于我们的运动或天体之间的相对运动。