在欧氏空间中，坐标系S和S′之间的相对速度为v，v的方向与共同的x-x′轴相同，且在t=t′=0时S和S′两坐标系是重合的。求S和S′之间在任意时刻的坐标关系。

根据欧氏空间的各向同性和运动学，很容易解出在任意时刻，两个对应参照系之间的坐标关系。

这就是伽俐略变换。

狭义相对论认为，麦克斯韦方程中常数是光在真空中的传播速度，真空中的光在所有惯性参照系中的速度都相同，都是常数c。洛伦兹变换符合光速不变假设，与麦克斯韦方程组即与电磁学相容，因此是正确的。根据伽利略变换，若光速在某惯性参照系中为c，而在相对速度为v的另一惯性参照系中，根据矢量加法光速应为c+v，与光速不变假设矛盾，与麦克斯韦方程组，即与电磁学不相容。在此伽利略变换不成立，被狭义相对论否定。

洛仑兹变换虽然满足光速不变原理，但是洛仑兹变换中的光速是矢量。如果将光速理解为矢量，光速不变与矢量加法矛盾，满足矢量加法，则必然不满足光速不变原理，伽利略变换属此；满足光速不变原理，则必然不满足矢量加法，洛仑兹变换即属此。然而奇怪的是，洛仑兹变换凭借前者将伽利略变换否定，而无视自身不满足矢量法则，并被奉为狭义相对论的基础。

光速定理和光子速度定理说明光速不是矢量，因此伽利略变换不满足光速不变原理是必然的、正常的。在不同参照系中光子速度满足矢量加法，这说明伽利略变换与光速不变相容，也与麦克斯韦方程和电磁学相容，因此“伽利略变换”是正确的，应予正名。伽利略变换有以下特点。

(1)利用伽利略变换，可以推导出欧氏空间中两个参照系间的基本时间单位“秒”和基本长度单位“米”的变换公式，且变换比相等，均为1，与光速定理相符，说明伽利略变换包含了两个参照系间的基本时间单位和基本长度单位的变换公式。

(2)利用伽利略变换可以推导出速度变换公式，即矢量加法公式，因此伽利略变换包含了速度变换公式。

伽利略变换可以作如下拓展。

如果参照系S和S′的相对速度为在t=t′=0时两坐标系重合，则伽利略变换可以表示为：

该式称作任意速度的伽利略变换。

如果在t′=t=0时，两天体的距离为x0，且相对速度为v，方向沿共同的x-x′轴的正方向，则伽利略变换为：

该式称作任意位置的伽利略变换。

假设坐标系S和S′的坐标轴分别平行，两坐标系存在相对变速运动。如果在坐标系S中考量S′的运动，可用S′的坐标原点O′在S中的运动表述：Ro′=Ro′(r、t)。(www.daowen.com)

如图7-1所示。如果某质点P在坐标系S′中的运动为：R1=R1′(r、t)，坐

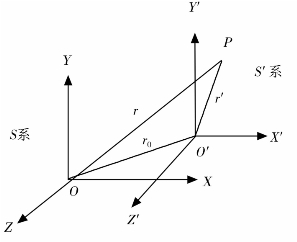
图7-1

标系S′的原点O′在参照系P中的运动为R0=R0(r、t)，则该质点在坐标系S中的运动可以表示为

式中的R0和R1都是加速运动，其轨迹是任意曲线，称作加速运动的伽利略变换，其式的分量式为：

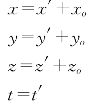
P点在S中的速度、加速度分别为：

(7-4)式说明伽利略变换的实质，是表示同一物体在任意两个坐标系中的运动关系，它将物体在某坐标系中的运动变换为任意坐标系中的运动提供了理论依据。

根据天体A、B相对于我们的光行差和多普勒频移，可以求出A、B分别相对于我们的运动为

根据这两式，可以求出A、B之间的相对运动为

根据上述三式中的任意两式可以求出第三式。这说明伽利略变换将宇宙中所有天体的运动都联系为一个有机的整体。洛伦兹变换则无法这样做，因为洛伦兹变换的空间和时间单位不同，并且不能解决任意方向速度和加速度的变换。