1.假设欧氏空间中物体A在方向不变的外力f(t)作用下做加速运动，f的方向指向x轴正方向

为了便于说明问题，假设参照系A和B的时间坐标相同，并且在t=0时物体A与物体B的相对速度为v0，v0的方向指向x轴的正方向。B位于坐标原点，A位于P(0、y0)，其中y0＞0，并且y0的绝对值非常大。光源A发出的单色光频率为ω。现在讨论光源A发出的光子在参照系B中的行为表现。

物体A在外力f(t)的作用下做加速运动，在任意时刻t的加速度为a(t)。根据矢量法则，这时AB之间的相对速度为方向为x轴方向。

根据牛顿运动学，光源A在t=t(t≥0)时向着y轴负方向发射的光子，在参照系B中的速度由两个方向的分速度组成。一是在x轴方向的分速度二是在y方向的分速度因此该光子在参照系B中具有速度

(1)式(6-3)是在t=t时从A向y轴负方向发出的光子速度方程。式中的t是指光子从光源A发出的时间，与B的坐标时间相同。对确定的光子，t是确定量而非变量。

(2)光子在发出后不再受到外力f的作用，该光子在发出后将始终以(6-3)式的两个分速度相对于B做惯性运动，即所有光子在参照系B中的运动轨迹都是匀速直线运动。不同光子x方向的分速度不同，这些光子组成的轨迹为曲线。

(3)确定的光子与物体A的x方向的速度值分离，不因A在x方向的速度值变化而变化。物体A在x方向的速度值为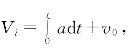它随时间t的流逝而变化；所有光子在发出后，x方向的速度值都不会变化，其值由发出时A在x方向的速度值确定。

(4)对不同的光子，式中的t值不同。对不同的t值，(6-3)式的第一项表示了光源从t=0起至t=t发出的，所有向着y轴负方向的光子在x轴正方向的不同速度。

(5)由于AB之间距离y0很大，t值不是很大时，光源A在x轴方向运动引起的、偏离y轴的变化可以忽略，即A、B在AB方向没有相对运动，观察者B接收到的频率没有变化。

(6-3)式所描述的，在不同时刻向着y轴负方向发射的光子行为，是根据光子速度定理和运动学得到的理论值，实际上观察者是不能观察到光子的速度的。观察者B可以根据接收到的光子信息，得出与光源相对运动状况的信息。

观察者B在某一时刻T接收到光源在t=t时刻(显然T=t+y0/c)发出的光子，根据(6-3)式和光行差和多普勒效应中的分析知道，T时观察者观察到光源A在t时刻的光行差为

这是理论值，其实际值可以根据光源A在天球上的自行计算出来。

假设通过观测，观察者B知道光源A在天球上的自行，因此观察者B在T1时观测到光源A在t1时刻的光行差为α1；T2时观测到光源A在t2的光行差为α2。根据光行差(4-11)式和(6-4)式，观察者B可以准确地确定在t1时刻A、B之间相对速度为方向为x轴正方向；在t2时刻，A、B之间的相对速度为方向为x轴正方向。从(6-4)式可以看出，随着时间T的推移，观察者B将观察到光源A的光行差随时间改变。如果观察者B坚持长期观察光源A的光行差，可以获得光源A在任何时候相对于观察者的光行差。如果这个光行差用函数表示，理论上它就是(6-4)式。观察者根据观测得到的某一时刻t光源A的光行差，根据光行差公式tgα=，求出光源相对于观察者的横向速度v。观察者B坚持长期观察光源A的光行差，可以获得光源A在任何时候相对于观察者的速度v。用函数表示，就是观察者B也可以求出光源A在任意时刻t相对于B的加速度的值。根据上述分析知道，如果这个相对加速度用函数表示，就是方程a=a(t)。

以上分析说明，在欧氏空间中，如果光源相对于观察者在两者连线的垂直方向做加速运动，则观察者仅凭接收到光源光行差变化就可以准确地获得光源相对于观察者运动的完整信息。

2.假设A是观察者，物体B是光源，其他不变(www.daowen.com)

现在考量光源B向着y轴正方向发出的光子，在参照系A中的表现。

A是观察者，就是以A为参照系。这时AB的位置与前一种情况互相交换，A在原点，B在(0、-y0)。根据矢量法则和牛顿运动定律，这时观察者A将观测到光源B以初速度v0、加速度a(t)向x轴负方向运动。在时刻t=t，光源B的速度为Vi=∫t 0adt+v0，方向指向x轴的负方向。由于A受到外力在欧氏空间中做加速运动，B没有受到外力作用。因此对于光源B向着y轴正方向发射的所有光子，根据矢量法则，它们由两个方向的分速度组成。一个向着x轴负方向。它们在x轴方向与光源B有相同的速度和相同的x坐标，这些光子和光源B一样都在相对于观察者A做加速运动，加速度均为-a(t)。因此，B与这些光子任何时刻在x方向的速度值都相同，均为方向指向x轴的负方向。另一个分速度向着y轴正方向，光子由光源B发出时，相对于B的速度始终为c，方向为y轴的正方向，所有光子相对于A都具有y方向的速度因此，t=t时所有光子在参照系A中的速度都相同。

(6-5)式与(6-3)式仅相差一个负号，其他完全相同，但是两者的内涵不同。

(1)若将某一光子从B发出的时刻t称作该光子的发出时刻，(6-5)式对所有已经发出的光子都成立，当然仅限向y轴正方向传播的，即(6-5)式是所有光子t=t时刻在参照系A中的速度。

(2)(6-5)式中的t是变量，根据假设，t≥0。

(3)AB之间的距离y0很大，在t值不是很大时，光源B在x轴方向运动引起的偏离y轴的变化可以忽略。即A、B在AB方向没有相对运动，观察者A接收到的频率没有变化。

(4)所有光子都有相同的速度，含x、y两个方向。所有光子相对于观察者A的运动都是加速运动，即所有光子在参照系A中的运动轨迹都是曲线，这些光子组成的轨迹也是曲线，与前述假设1中B观测到的轨迹完全相同。

(5)在同一时刻，所有光子的x坐标相同，y坐标不同，所有光子的轨迹都相似。同样，(6-5)式描述的不同光子行为，是根据光子速度定理和运动学得到的理论值，实际上观察者A是不可能观察到光子的速度的。在这种情况下，观察者A可以根据接收到的光子信息得出什么结论呢?

观察者A在某一时刻T，接收到B在t=t时刻发出的光子，根据(6-5)式和光行差和多普勒效应的分析知道，在T时刻观察者A观察到光源B的光行差为

这是理论值，其实际值可以根据光源B在天球上的自行计算出来。

假设通过天文观察观察者A知道光源B在t=0时在天球上的实际位置，并且假设观察者A在T1时观测到光源B在t1时刻的光行差为α1；T2时观测到光源B在t2时刻发出的光行差为α2。根据光行差公式(4-11)α=和(6-4)′式，观察者A可以准确地确定在t1时刻A、B之间的相对速度为V=方向为x轴负方向；在t2时刻，A、B之间的相对速度为adt+v0，方向为x轴负方向。由于(6-4)′式和(6-4)式完全相同，因此在这种情况下观察者A长期坚持观测光源B的光行差获得的信息和假设1完全相同，结论也完全相同。

比较两种方法，说明在欧氏空间中，若A、B两物体在其连线的垂直方向的运动为加速运动，无论是A做加速运动，或是B做加速运动，无论以A为参照系考量B的运动或以B为参照系考量A的运动，都可以得到以下两个结论。

一是观察者仅凭接收到光源的光行差变化就可以获得光源相对于观察者在与AB连线垂直方向运动的正确、完整信息。

二是观察者得到的结果都与观察者不动，是光源相对于观察者做加速运动的结果相同。