在不同参照系中，谱线能量关系怎样呢?假设某一单色光在某一参照系中频率为ω1，在另一参照系中频率改变为ω2，有(5-21)式表示，同一单色光在不同参照系的能量比等于其频率比，同样等于其光子数之比。(5-20)式和(5-21)式虽然完全相等，但是二者的内涵是不同的。前式表示的是不同的两光谱线在同一参照系的能量比等于其频率比；后式表示的是同一光谱线在不同参照系的能量比等于其频率比，其实质都是光子的数量比。后式还说明，同一光谱线在不同的参照系频率改变了，仅是单位时间接收到的光子数量改变了，谱线总的光子数量并没有改变，即总能量和总质量是守恒的。由于频率也可以表示光子的数量，因此这两式还说明光子在所有参照系中的能量是相同的，都是h。这个结论与(5-19)式的结论相同。

光子在所有参照系中的能量都相同。这是因为只涉及一个参照系时，该参照系就是光子的本征参照系，其速度值都相同，即C=c。设光子的质量为μ，光子的动能为

表示光子的能量性质是动能。

同一光子在不同参照系中，其能量关系怎样呢?从逻辑上讲，既然光子在概念上是粒子，就应该具有粒子的属性。同一粒子在不同参照系中的速度不同，能量也不同。同一光谱线在不同的参照系中频率不同，从光子的角度而言即为速度不同，则同一光子在不同参照系中的能量必然不同。为了讨论这一问题，先看下面的例子。

例一：情况1，有一挺机枪每一秒钟发射f发子弹，子弹之间的距离为L。观察者以速度v1向机枪靠近。情况2，有一光源发出的单色光频率为ω，观察者以速度v2向光源靠近。

问：以上两种情况，子弹与光子的有关物理量有何相同、有何不同?情况2中光子相对于观察者参照系的能量是多少?

对于第一种情况，是以机枪所在参照系为本征参照系。子弹与机枪的相对速度为u=fL，根据矢量加法，子弹与观察者的相对速度为u+v1。观察者观测到子弹的频率为即子弹之间的距离相对于机枪和观察者都相同，都是L。子弹相对于机枪的动能是子弹相对于观察者的动能是增加的动能为

对于第二种情况，根据光在欧氏空间中传播的结论，光子相对于光源的速度为c，相对于观察者的速度为c+v2。在光源参照系中光子之间的距离(波

长)为λ=，在观察者参照系中光子之间的距离为说明在光源和观察者两个参照系中光子之间的距离即波长不同。结果与情况1中子弹之间距离相对于机枪和观察者都是相同的结果不同。不同的原因是在情况1中始终以地面为参照系；情况2的波长则分别以光源和观察者为参照系。因此情况2中光子相对于观察者参照系的动能不能为

例二：设某物体在A点的初速度为v，到达B点时动能增加了ΔE。该物体在B点时的动能变成多少，速度变成多少，增加了多少?(www.daowen.com)

物体的初动能为获得的动能为ΔE，令物体的动能变成该式说明u、v和Δv的值组成一个直角三角形，无论u、v和Δv的方向相同或不同，它们的值满足勾股定理。反之，无论u、v和Δv的方向相同或相反，它们的值都不能直接相加减。即v+Δv≠u；或者，v+Δv＞u。即在u、v和Δv的方向相同或相反时都不满足矢量法则。

例二和例一的情况1有明显区别，情况1中子弹相对于观察者的能量由子弹相对于观察者的速度u+v1确定；例二中物体的能量由初始能量E0和增加的能量ΔE确定。例一的第二种情况实际上和例二相同，光子的动能也应该由初始能量E0和增加的能量ΔE确定。例一的第二种情况中，光子相对于光源的速度为c，能量为

观察者与光源的相对速度为v，则能量增加值为

因此光子在观察者所在参照系的能量为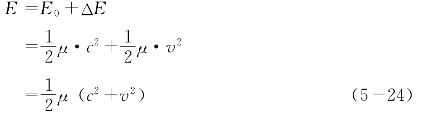

(5-24)式说明光子作为粒子，它在不同参照系中能量守恒，与其他粒子完全一样。式中的速度v没有大小限制，可以v≥c，该式虽然是从一个例子得到，但具有普遍意义。如果两个参照系以速度c相对运动，其中一个是光子的本征参照系，则光子在另一个参照系中的能量为光子在这个参照系中的速度为

从(5-24)式可以看出，光子在不同参照系中能量的三个速度值c、v、C满足勾股定理，即使它们的方向相同也一样。

上式说明，C≠c+v。

在“光子速度定理”中，同一光子在另一个参照系中的速度是C=c+v，其速度c和v是直接相加，光子速度满足矢量法则；现在计量光子在另一个参照系中的能量，涉及的速度不能直接相加，不满足矢量法则，它们的关系满足勾股定理。同一现象产生不同结论的原因，缘自光速不变和光的波粒二象性，它彰显了光子的奇异性。因此，不能用对待一般粒子的定式思维看待光子。在物理学范围内，我们不能证明以上两种结果的光子速度孰对孰错，因为，它们依据的都是光速不变原理和光的波粒二象性。

上述结论也符合玻尔的“互补原理”。玻尔认为，在微观领域中运用一部分经典概念，同时会排斥另一部分经典概念，但是这些经典概念却在另外条件下说明现象同样是不可缺少的。这些经典概念之间互为补充，并不是互相排斥的。玻尔称“互补原理”是反复思索的结果，是从自然界中探求到的一个积极成果。