观察者与光源在其连线方向(以下简称纵向)存在相对运动时，会观察到光的频率(波长)有改变。这一现象称作多普勒效应，也称作“多普勒频移”。

当观察者和光源互相背离时，多普勒频移公式为：

或

式中，ω′和λ′为本征频率和本征波长，ω和λ是观察者观察到的频率和波长，v为观察者与光源的相对速度。在这种情况下，谱线的波长变长，频率变小、向红端移动。

多普勒红移：观察者接收到的波长与本征波长比较时，波长变化的相对量。

多普勒红移用公式表示就是z=(λ-λ0)/λ0，其中z是红移的值，λ0是光源发出的谱线的本征波长，λ为接收到的波长。根据(4-2)式，多普勒红移为：

如果0≤v≤c，则0≤z≤1；如果v≥c，则z≥1。

多普勒红移使用极为频繁。在天文观测时，每一个可以观测到的天体都必然，且必须观测其发射光中可以辨认的光谱线，从而确定其本征频率或本征波长，再根据接收到的频率，利用多普勒公式确定其与我们的相对速度。比较远的天体还可以用多普勒红移确定其与我们的距离。当观察者和光源互相靠近时，多普勒频移公式和波长公式为：

(4-4)式和(4-5)式中，ω′和λ′、ω和λ及v的意义与(4-1)式、(4-2)式相同。在这种情况下，谱线的波长变短，频率变大，向紫端移动，其多普勒红移为：

这种情况又称为(多普勒)紫移或蓝移。如果0≤v≤c，则0≥z≥-1/2；如果v≥c，则z≤-1/2。

公式(4-1)、(4-2)、(4-4)、(4-5)统一称为“视线方向的多普勒公式”，以和后文的“任意方向的多普勒公式”区别。

天球：在天文观测中，将我们观察到的整个天空背景想象为一个球面，假设所有天体都镶嵌在以观察者为球心、以一定长度为半径的球面上，这个球面称为天球。

视位置：观察者观察到的天体在天球上的位置。

光行差：当光源和观察者在二者连线的垂直方向(以下简称横向)有相对运动时，会观察到光源的视位置与其实际位置不一致。这一现象称作光行差效应，其视位置与实际位置的差角称为光行差角，简称“光行差”。

光行差定理：当光源和观察者在二者连线的垂直方向相对速度为v时，将观察到光源的光行差记为α，且tgα=v/c。

证明：设光源S以速度v相对于观察者A做相对运动，v的方向与光源的光线垂直且指向左面。在图4-1中，BD是光源运动方向，速度为v。BO是光源光的实际传播方向。OS是光源的实际方向，也可以理解为S是光源在天球坐标上的实际位置。A是观察者在某一时刻的位置。(www.daowen.com)

根据牛顿运动学，光源S向左面运动就是相对于光源不动观察者向右面运动。假设AO是观察者在某一单位时间的运动轨迹。在天文观测中，光源与观察者的距离通常都非常远(一般都在若干光年以上)，因此光源S发出的光线在到达AO时，都是与AO垂直的平行光。或者说光源发出的球面波到达AO附近时，其波阵面已经完全与AO平行。若光源发射的球面波的频率为ω′、波长为λ′，则这些球面波是以λ′为间隔均匀地分布在直线BO上的。根据光速不

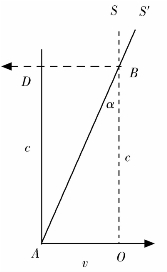
图4-1

变公理有ω′λ′=c。由于观察者与光源在其连线的方向没有相对运动，任何时刻到达O点的波阵面，都是同一时刻到达AO一线的同一波阵面，因此观察者在AO这一路上接收到的频率与O点接收到的频率完全相同。又由于O点与光源没有相对运动，O点接收到的频率、波长与光源的发射频率、波长相同，因此观察者接收到的频率、波长也与光源的发射频率、波长相同。即：

所以

在这种情况下光速定理同样成立。

此时，光源的相对速度v在观察者和光源连线方向的分速度为0，这也是多普勒公式中v的意义。因此在这种情况下的多普勒定理同样成立，同样以(4-7)、(4-8)两式表征。

假设观察者在O点接收到的光子一秒钟前位于B点，而观察者一秒钟前位于A点。连接AB，根据矢量法则，在观察者看来，BA就是光子相对于自己的速度。根据光速公理和前面的假设，有BO=ω′λ′=c。光子相对于光源的速度与光速相同，即C′=BO=c，光源相对于观察者A的速度是OA=v。根据矢量加法，光子相对于观察者A的速度为：

(4-9)式说明，在图4-1的情况下光子速度定理同样成立。当观察者在A点时，该时刻位于AB一条线的光子，在观察者从A向O运动的过程中，将悉数被观察者接收。因此观察者将认为光源的光是从BA方向传播来的，AB方向就是光源的视位置方向，即观察者观察到光源在AS′方向，而OB的方向是光源的实际位置方向。设α=∠OBA，则：

这就是当观察者和光源相对速度方向与光传播方向垂直时的光行差公式。其中，α就是这种情况下的光行差，表示光源实际入射方向与观察者观察到的入射方向差角，在天文学上又表示光源(天体)在天球上的实际位置与视位置的距离，天体在天球上的位置是用经纬度表示。光行差公式的推导说明，光行差与光的频率、波长无关，它体现了光的粒子性。光行差效应的本质是光的粒子性的宏观表现。事实上，如果将光子看作雨点，(4-10)光行差公式和观察者在雨中行走时看到雨点方向的改变完全相同。如果v与c相比很小，有：

从推导可以看出，公式(4-10)、(4-11)中c的意义是光子速度，是光子相对于光源的速度矢量，满足矢量法则，不是ω×λ之积。

证毕。

在天文观测中，光行差现象是很普遍的。如果观测对象不同，地球与之相对速度就不同，其光行差也不同。光行差中最重要、最著名的是周年光行差，即地球公转产生的光行差。现在计算其大小：地球的公转轨道长2π×1.5×1011m，运行时间为86400×365.2422s，由此可以算出地球公转的线速度约30km/s，利用光行差公式(4-10)可以算出地球公转的光行差，即周年光行差约为20.5″。地球公转速度方向的变化以1年为一个周期，可以观察到恒星在天球上的视位置是一个以1年为周期，直径约为20.5″的圆。同样，可以计算出周日光行差——地球自转造成的光行差，比周年光行差小两个数量级，约为零点几角秒；另外，在实际的天文观测中还有以下重要的光行差。

长期光行差——太阳系在宇宙空间中的运动造成的光行差，包括太阳本动造成的光行差，约为13角秒，但方向不变；太阳系绕银河系公转造成的光行差，约为100多角秒，但周期很长。

以上光行差都是地球、太阳、太阳系、银河系之间的相互运动造成的。如果对河外天体观测，应根据情况将上述光行差作适当扣除，才能得到该天体在天球坐标中的正确位置。