根据“光速定理”，任意一个波包相对于所有参照系的速度都是光速；而根据“光子速度定理”，光子速度满足矢量法则，即同一光子相对于不同的参照系，仅与某一参照系的速度为c，与其他参照系的光子速度都不同。因此确定光子速度应遵循一定的原则。下面讨论这个问题。

在证明光子速度定理时，图2-1表示观察者与光源以速度v互相靠近的情况，是假设光子与光源S′的相对速度为c，计算出光子与观察者S的相对速度为c+v，证明光子速度满足矢量法则的。现在，假设光子与S的相对速度为c，看看光子与S′的相对速度是否为c-v，从而判断与矢量法则的结果是否一致。

假设光子在S中的速度为c，是以S为参照系，即应该以光相对于S的波长作为计算基础。S′每秒钟发出ω′个波包，因此S′每秒钟发出的光的长度，即光与S′的相对速度：这个例子说明，如果设置不当，由相应的频率和波长确定的光子速度，在不同参照系中的值不满足矢量法则。

相对于图2-3观察者与光源以速度v互相背离的情况，如果假设光源S′与光子的相对速度为c，同样可以计算出观察者S接收到单色光的长度，即光子相对于S的相对速度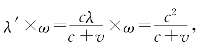与图2-1假设光子与S的相对速度为c时得到的结果完全相同，因此光子速度一般不能随意设置。为此，提出以下设置光子速度的原则：

(1)如果涉及两个参照系中光波的频率时，应该将其中频率较小的参照系中的光子速度设置为c，即C1=c；将频率较大的参照系中的光子速度设置为C2=c+v。换言之，如果涉及频率，则光速是光子速度的下限。

(2)如果不涉及光的频率和波长，例如光源发出的只是光脉冲，则无上述限制。这种情况下，一般将相对于观察者的光子速度设置为C1=c，光源所在参照系中的光子速度设置为C2=c+v，其中v可以是任意方向的速度矢量。也可以根据情况将光源所在参照系中的光子速度设置为C1=c，将观察者所在参照系的光子速度设置为C2=c+v或C2=c-v。

(3)如果只有一个参照系，不涉及其他参照系，应将光子速度直接设置为C=c。

上述光子速度的设置原则也称作“光速与光子速度的关系”。为什么对相同的波包，分别将其看作光子或波的相位时的速度不同呢?事实上两者这时扮演的角色有本质区别。

当将波包看作光子时，一个波包就是一个光子，即一个粒子。光子速度是由一个光子确定的，与其他光子无关。在任何确定时刻，任何一个光子都必然有确定的位置，因此它相对于任何确定的物体(参照系)都有确定的速度，并且这些确定的速度都彼此不同。另一方面，根据量子理论，光子是粒子。就粒子的内涵而言，粒子的速度具有矢量属性是量子的特征。即只要是粒子、是质点，它的线速度一定满足矢量法则。因此，光子速度满足矢量法则是必然的。这说明光子的本质是质点，是物质。

当将波包看作波的相位时，单个波包没有确定的波速。波速必须是若干波包共同的集体行为，并且所谓“若干波包”是以可测量出的光波波长和频率为下限。如果不能测量出光波的波长和频率，光波的波速就是不确定的，因为光速的概念是波长与频率之积。

上面的分析还说明，可以将光的波前或脉冲的速度看作光子速度。因为它们在确定的时间有确定的位置，相对于确定的物体有确定的速度。

“光速定理”说明：光速λω=λ′ω′=c中的λω和λ′ω′表示的都是光在单位时间包含的周期数(频率)所具有的长度(距离)。它们只有在各自本征参照系中的值才是c。因此光速与参照系无关，即与物体的运动状态(速度、加速度等)无关。因此ct表示的距离也与物体的运动无关。例如，金牛座α星，中国称为“毕宿五”，距离地球约65光年。该距离是“毕宿五”65年前的空间位置与地球现在空间位置之间的距离。“毕宿五”在65年前已经离开那一位置；地球是现在才到达现在位置。因此两个位置之间的距离是绝对空间中两点的距离。绝对距离与相对距离有本质的不同：表征相对距离的两点可以在空间中移动，例如地球与太阳之间的距离。由于太阳与地球的运动，二者之间的距离就有变动，表征距离的两点也有变动；而表征绝对距离的两点是绝对空间中的点，它不会在绝对空间中运动。相反，运动是质点相对于这些空间中点(位置)的运动。绝对距离与物体之间的运动无关，因此，光速是相对于绝对空间的绝对速度，是光波宏观运动的本质。

在第四章“任意方向的光行差和多普勒效应”中我们可以看到，光子速度C=c+v中的v可正可负，可以是任意方向的，其大小也没有限制，可以数倍于光速c，C的值也可以小于零。由于光子速度是光子相对于质点的理论速度，因此，光子速度是相对于相对空间的相对速度，是光子粒子性的宏观属性。

例1：假设地球O现在接收到天体P在单位时间前发出的光，地球与天体的相对速度为V。则二者的时空关系可以由图2-5表示。

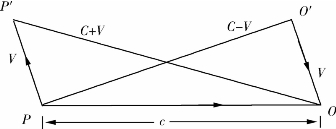
图2-5

图2-5中，地球观察者O认为自己一直在O点，接收到天体P在P点发出的光。根据“光速定理”，光子相对于O的速度为C=c，即PO=c。P在此后以速度V运动到P′点，即PP′=V。根据矢量法则，地球观察者认为光子相对于天体P的光子速度为：。另一方面，天体P上的观察者根据地球在O点接收到自己在P点发出的光，认为光子相对于自己的速度是C=c，即PO=c。观察者P认为自己一直在P点，是地球在单位时间前以相对于自己的速度V从O′运动到O点，并且在O点接收到光子。因此，观察者P认为光子相对于地球O的速度为

这个例子完全颠覆了运动学中相对运动的概念。从图2-5可以看出，如果将光的运动一并考虑，天体P与地球之间的运动并不是相对运动。如果将P、P′、O、O′看作绝对空间中的点，则天体P与地球都是相对于绝对空间运动。事实上，仅就天体P与地球的关系而言，二者之间的关系仍然是相对运动。假设天体P相对于绝对空间的速度为vp，地球相对于绝对空间的速度为v0，这里的vp、v0均不等于V，并且方向可能不平行，则天体P与地球的相对速度为：

上式表明两物体之间的相对速度为两物体与绝对空间的绝对速度矢量差。这个结论虽然是从一个例子归纳得到，但具有普遍意义。后面第七章的“王氏第二运动定理”的推论说明，绝对加速度与相对加速度同样存在与该公式类似的关系。(2-7)式说明绝对运动是相对运动的本质，相对运动是绝对运动的表现形式。

这个例子还可以得到四点结论。

(1)在图2-5中，可以认为光源P在经过P点时发出的光波沿着PO传播，在单位时间后到达O点，被恰好经过O点的地球接收到。因此PO是绝对空间中的绝对距离。在距离公式L=ct中，t是绝对时间，L是绝对距离，c是光波相对于绝对空间的绝对速度。天文学中的光年表示的是绝对距离。这是光速与光源和观察者的运动状态无关，即与参照系无关的时空学本质。

(2)光子速度c+v与物质之间的相对速度v始终是分离的。在一般情况下光子速度满足矢量法则仅仅是理论上的、形式上的。

(3)如果将图2-5中光波从P到O的传播，看作是波前或光脉冲(即看作光子)，PO就是光子在单位时间移动的距离。因此在本质上任何一个光子相对于绝对空间的绝对速度始终为c。

(4)光的波动性是光子的宏观表现形式，光子是光波的量子本质。(www.daowen.com)

上述分析还说明，物理公式中出现的c+v或c-v，其中的c本质都是光子速度，量纲是速度，只是数值与光速相同。因为，只有矢量速度才可以互相比较(相加减)。

根据“光子速度定理”，可以将相互靠近或退行的多普勒公式合并为一个。设ω′、λ′、C′分别表示单色光的本征频率、本征波长、本征光子速度，ω、λ、C分别表示单色光在观察者参照系的频率、波长、光子速度。于是，公式(2-1)和(2-4)可以表示为：

公式(2-2)和(2-3)可以表示为：

根据(2-8)、(2-9)式，多普勒定理也可以表述为：若观察者与光源的相对速度为v，光源发出的单色光频率为ω′，波长为λ′，则观察者接收到的频率与参照系中的光子速度成正比，接收到的波长与光子速度成反比。

该表述揭示了多普勒频移的本质，多普勒频移的原因是光子与物体的相对速度改变了。若光子的相对速度增大，则光的频率增大，波长变短；若光子的相对速度减小，则光的频率减小，波长变长。这与粒子之间相对运动的结论是相同的，例如可以将光的频率理解为机枪发射子弹的频率。

这样，运用光子速度的概念，多普勒定理的物理意义更明确、公式更简单、表述更简明。

(2-8)和(2-9)式可以利用地球绕日公转运动验正。对某一位于黄道附近的恒星P，假设太阳S与P连线方向的相对速度为v0，二者互相背离，地球的公转速度为v.则在v0和v互相垂直时，对该恒星发出某一波长为λ的谱线，地球接收到的波长λ′如图2-6中的B、D点，为

当地球的公转方向向着恒星时，如图2-6中的A点，假设v0-v＞0，地球接收到的波长为：

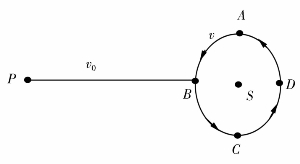
图2-6

当地球的公转方向背离恒星时，地球接收到的波长如图2-6中的C点，为

其中，(2-11)式是地球上可以接收到的该恒星谱线的最小波长，(2-12)式是地球上可以接收到的该恒星谱线的最大波长。

根据以上三式可以发现，

若黄道附近的恒星，在图2-6中A、B、C、D点的接收频率ω′、ω1′、ω2′均大于本征频率ω，说明该恒星是以速度v0与太阳靠近，并且v0＞v，其中v为地球公转速度。在这种情况下，以上三式应该用频率公式表示。

在一年内，地球接收到黄道附近的恒星谱线的波长将在λ1′～λ2′或谱线的频率将在ω1′～ω2′范围内波动。因此λ1′～λ2′或ω1′～ω2′称作“某恒星某谱线的周年频移带”，简称“周年频移带”。与此相同，在黄道附近的脉冲星的“脉冲频率”也存在周年波动现象。为讨论方便，我们将每秒钟接收到脉冲星的脉冲次数称作“脉冲频率”n，将L=称作“脉冲波长”。假设在黄道附近的某一脉冲星，在地球公转方向与该星和太阳连线方向垂直时，如图2-6中的B、D点，接收到的脉冲频率为n′次/秒，得到在该位置接收到的脉冲波长为L′。则在地球公转的A、C位置可以测量出该脉冲星的频率为n1′、n2′或波长为L1′、L2′。如果满足L1′+L2′=2L′，则说明该脉冲星与太阳互相背离。根据公式(2-10)、(2-11)、(2-12)中任意两个，可以求出脉冲星的本征脉冲波长L和与太阳的视向速度v0；如果满足n1′+n2′=2n′，则说明该脉冲星与太阳互相靠近。根据公式(2-14)、(2-15)、(2-16)中任意两个，可以求出脉冲星的本征脉冲频率n和与太阳的视向速度v0。

以上是关于脉冲星测量的最新观点。利用这个实验可以检验多普勒定理、光速定理、光子速度定理的正确性。