在这一节，我们把加权分位数回归方法、加权复合分位数回归方法与最小二乘方法进行比较，并运用到Melbourne CPI数据集，该数据可从澳大利亚统计局（www.abs.gov.au）下载。数据收集了从1972年9月到2016年9月期间共N=176组样本。我们主要探索All groups CPI（Y）和8个记录的变量之间潜在的关系：食品和非酒精饮料（X1），酒精和烟草（X2），衣物与鞋类（X3），住房（X4），家具、家用设备和服务（X5），运输（X6），通信（X7），教育（X8）。记X=（X1，…，X8）T，时间变量U=（1/N，2/N，…，1）T。注意到当且仅当Y≥31时（Y，X，U）才能观察到且可观察到子集的元素个数是138，因此该数据集的截断率为21.591%。

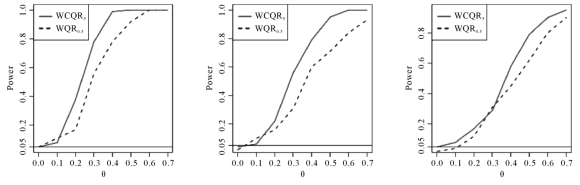
图5-4　基于WQR0.5和WCQR5的检验统计量Tn在三种误差分布下的功效曲线：标准正态（左），混合正态（中）和t（3）（右）。

利用下列的变系数模型

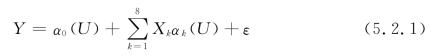
来拟合数据。我们的估计基于Epanechnikov核，τ=0.50时，最优窗宽hopt=0.35。Bootstrap检验重复次数为500。首先，利用基于bootstrap的检验程序来检验模型（5.2.1）是否是线性模型，即检验

H0：（α0（U），αT（U））T=θvs H1：（α0（U），αT（U））T≠θ，

其中θ是未知的参数向量且α（·）=（α1（·），…，α8（·））T。借助WCQR5估计方法，得到θ的估计量是(www.daowen.com)

假设检验的p值是0，故在显著性水平α=0.05下，拒绝模型是线性模型的假设。因此协变量的系数应被假设为变系数的，故使用变系数模型（5.2.1）来拟合Melbourne CPI数据。预测误差被用来评价5种估计方法的相对有效性，其定义为，是Yi的拟合值且A=｛kYk≥31｝。预测误差的结果见表格5-3。进一步，基于LS，WQR0.5和WCQR5方法的未知函数的估计曲线见图5-5。

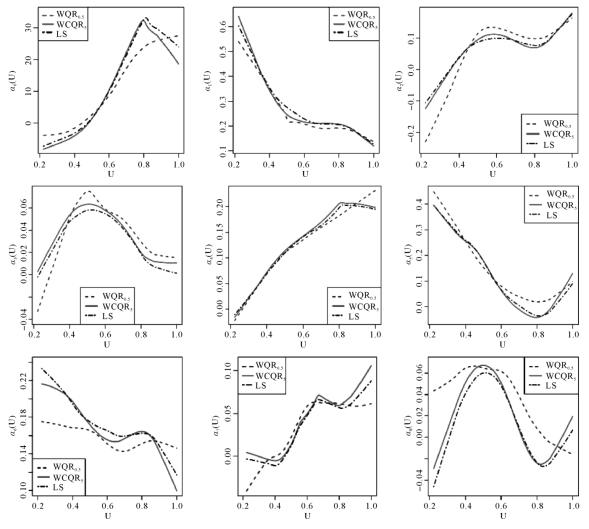
图5-5　基于三种估计方法的非参数函数的估计曲线

表5-3　Melbourne CPI数据的预测误差结果

由表格5-3，可以发现：加权复合分位数回归方法的预测误差最小。故它的表现最好。图5-5给出了9个函数关于时间变量U的变化趋势。例如，α4（U）是正的且随着时间的增加而增加，这是合理的，因为近年来住房的影响越来越大。其次，α1（U）的曲线表明食品和非酒精饮料的影响越来越小。再者，α3（U）和α8（U）的CQR的估计曲线表明衣物与鞋类和教育对CPI的影响在U=0.5（即1994年8月）时开始都减小，而教育的影响在2008年8月以后越来越大。