在这一节，将通过模拟研究来评价提出的加权分位数回归估计量、加权复合分位数回归估计量以及基于bootstrap的检验方法在有限样本下的表现。核函数为Epanechnikov核K（u）=0.75（1-u2）+。假定N=300是固定的且观察到的样本n是随机的。（同样，也可固定n且容许N随机）模拟重复100次。本节通过采取τ=0.5时使得中位数平方误差（Median square error，MDSE）的平均达到最小来选取最优窗宽hopt。（见Cai等人（2000））。

注意到截断数据下F和G的乘积限估计量依赖Cn（·），Cn（y）在数据范围内可能为0，这会导致Fn（y）和Gn（t）在有限样本下的估计不合理，因此加权的分位数回归估计方法和加权的复合分位数回归估计方法可能会受到影响。故在模拟部分用

替代（5.1.2）中的Cn（y）。

例1　考虑下列的变系数分位数回归模型

Y=α0（U）+α1（U）X1+α2（U）X2+（ε-Qε（τ）），

其中X=（X1，X2）T～N（（0，0）T，I2），I2是2×2单位阵。U～U（0，1），α0（U）=4+sin（6πU），α1（U）=2cos（2πU），α2（U）=4U（1-U），Qε（τ）是ε的τ分位数。对ε，考虑5种不同的分布：N（0，1）；对数正态分布lnN（0，1）；非中心的t分布nct（3，2）；卡方分布χ2（2）和F分布F（4，6）。在本例中，为方便起见，固定N=300，截断变量T是根据均值为λ0的指数分布独立产生，λ0的选择见表格5-1，确保在不同的误差分布下，样本数据的截断率大约是10%和30%。

首先，表格5-1给出了信噪比。由表格5-1可以看到，在相同的误差分布下，对不同的τ和截断率，信噪比几乎相等。其中信噪比（Signal-tonoise ratio，SNR）的定义为

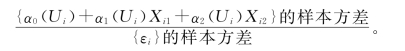
未知函数的估计量的表现通过下列的平均平方误差（average square error，ASE）来评价，

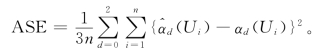
基于不同的τ，在两种截断率下，我们利用omniscient分位数回归方法（Omniscient quantile regression，OQR），本章提出的加权的分位数回归方法（WQR）以及naive分位数回归方法（Naive quantile regression，NQR）来评价未知函数估计量的平均平方误差。Omniscient估计量是在完全数据下通过分位数拟合获得，其样本量为N。Naive估计量是在截断数据下运用分位数回归获得，其样本量为n。进一步，在τ=0.50时，本节还比较了加权的分位数回归方法和最小二乘方法（LS）。非参数函数估计量的平均平方误差见表5-1。

图5-1（其样本来自例1）在三种误差分布以及两种截率下，给出了α1（U）在OQR方法、WQR方法、NQR方法以及最小二乘方法下的估计曲线。而且，为了给出条件分位数估计一个更直观的表现，在图5-2中，下面给出了，u=（1/n，2/n，…，n/n）的散点图，真实的分位数曲线图以及估计的分位数曲线图。

由表5-1和图5-1，有如下发现。首先，Omniscient估计量的表现最好，因为它使用了所有的样本数据。其次，当误差服从标准正态分布且τ=0.5时，最小二乘方法稍微比加权的分位数回归方法好一点。然而，在误差是其他几种分布的情况下，加权的分位数回归方法比最小二乘方法好。主要的原因是最小二乘方法对异常值非常敏感，而分位数方法在大多数情况下比较稳健。再者，当τ固定时，随着截断率的增加，加权的分位数回归估计量和Naive估计量的平均平方误差变大。而且，图5-1表明：加权的分位数回归方法可以很好的估计条件分位数。

表5-1　不同误差分布下，例1中ASE及SNR的均值

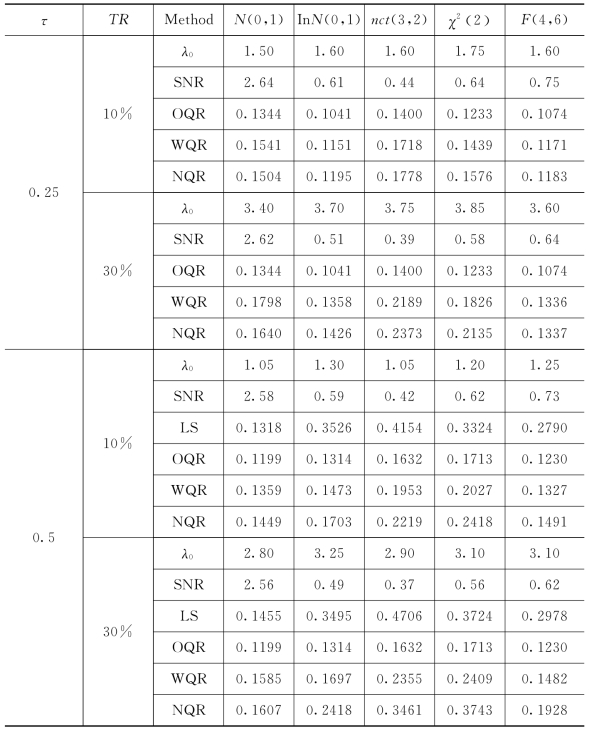
续表

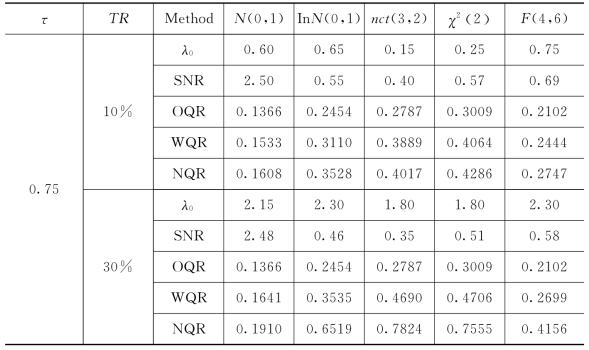
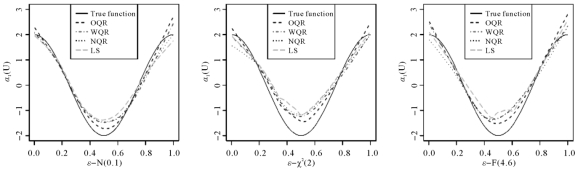
图5-1　α1（U）在三种误差分布下的估计曲线，TR=30%，τ=0.5。

例2　在此例中，给定τ=0.50，比较加权复合分位数回归方法（WCQRq）、加权分位数回归方法（WQR0.5）和最小二乘方法下的估计量的表现。进一步，为了检查加权复合分位数回归估计量中q变化产生的影响，考虑q=5，9，19。数据来自下列模型

Y=α1（U）X1+α2（U）X2+ε。(www.daowen.com)

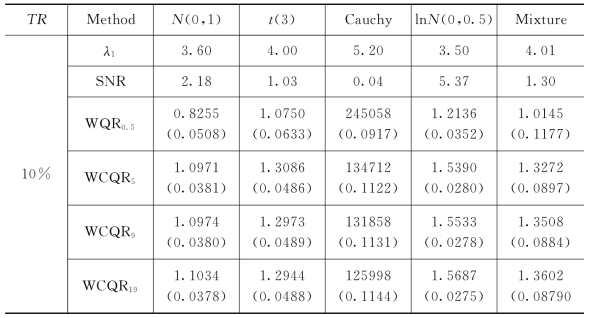
反应变量，协变量和非参数函数同例1。对ε，考虑5种误差分布情形：N（0，1）；t（3）；柯西分布；对数正态分布ln N（0，0.5）以及混合正态分布0.9N（0，1）+0.1N（0，102）。在下列模拟中，调整对数正态分布的均值，使其为0。截断变量T～Exp（1）-λ1，其中λ1的选取见表5-2，使得在不同情形数据截断率大约为10%和30%。信噪比结果见表5-2。

表5-2给出了加权分位数估计量或复合加权分位数估计量同最小二乘估计量基于平均平方误差的比较。其中N=300，每个模拟重复100次，平均平方误差比（the ratio of average square error，RASE）的定义如下

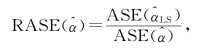
其中表示加权分位数估计量或加权复合分位数估计量是最小二乘估计量。若大于1，则优于最小二乘估计量，反之亦然。进一步，为了用图形显示结果，基于形状参数为1，尺度参数为0.5的Weibull分布，图5-3给出了基于5种估计量的箱线图。当ε服从Weibull分布时，λ1分别取3.45和1.89，使得数据的截断率大约为10%和30%。

由表格5-2和图5-3，可以发现：第一，除标准正态分布，在其他几种分布下，加权分位数回归估计量和加权复合分位数回归估计量比最小二乘估计量的表现好。潜在的原因是，在有异常值的情形下，加权分位数回归方法和复合加权分位数回归方法比最小二乘方法稳健。第二，对其他的误差分布，加权复合分位数回归估计量的表现最好，有最小的均方误差和最大的均方误差的相对率，最小二乘估计量的表现最差。这并不奇怪，因为加权复合分位数估计量包含多个位置的信息，因此能改进非参数函数估计量的有效性。第三，当误差分布对称时，q的变化对加权复合分位数估计量的均方误差和均方误差的相对率的影响最小；随着q的增加，加权复合分位数估计量的表现越好。第四，对每一种估计方法和给定的误差分布，截断率越小，估计量的表现越好。综上所述，在实际应用中，尤其是有异常值时，推荐使用加权复合分位数回归方法。

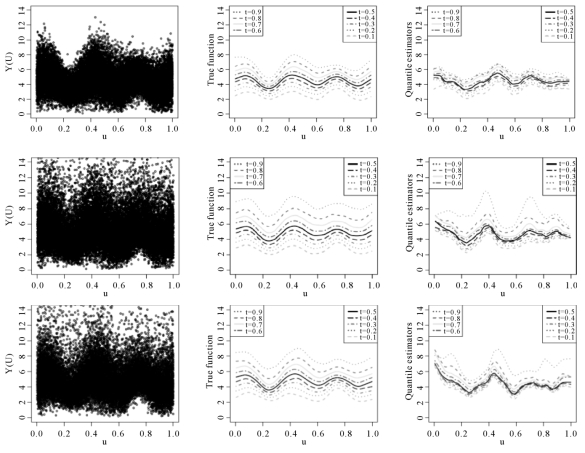
图5-2　误差服从N（0，1）（第1行），χ2（2）（第2行）和F（4，6）（第3行）及τ=0.5下的散点图（第1列），真实的分位数曲线（第2列）和估计的分位数曲线（第3列）。

表5-2　例2中RASE及SNR的均值（括号中为ASE的均值）

续表

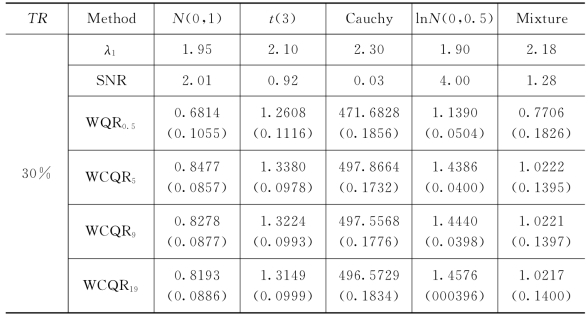
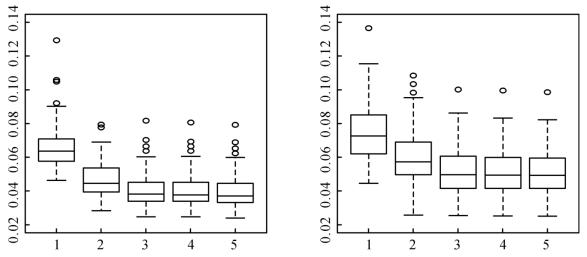
图5-3　基于5种估计量的Weibull分布下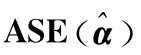的箱线图：TR=10%（左），TR=30%（右）。“1，2，3，4，5”分别代表以下五种估计方法“LS，WQR0.5，WCQR5，WCQR9，WCQR19”

例3　为了评价基于Bootstrap检验方法的性能，考虑左截断数据下的变系数模型：

Y=a（U）X+ε，

其中X～N（1，1），U～U（0，1），截断变量T～Exp（1）-3。考虑三种不同的误差分布：N（0，1），0.9N（0，1）+0.1N（0，102）和t（3）。真实的系数函数为α（U）=4U（1-U）+θ，且θ=0，0.1，0.2，0.3，0.4，0.5。我们的目的是检验

H0：α（U）=4U（1-U）vs H1：α（U）≠4U（1-U）。

样本容量、模拟重复的次数以及Bootstrap重复次数都为100。显著性水平α=0.05。

图5-4给出了检验统计量Tn基于WCQR5和WQR0.5的功效曲线。从中观察到：在所有情形中，基于WCQR5和WQR0.5的检验统计量Tn的功效随着θ的增加而增加；对固定的θ，基于WCQR5的检验统计量的功效比基于WQR0.5的检验统计量的功效大，故基于WCQR5的检验统计量比基于WQR0.5的检验统计量的表现更好。具体地，当原假设成立且误差服从标准正态分布时，基于WCQR5和WQR0.5的检验统计量的经验水平均为0.05；当误差服从混合正态分布时，基于WCQR5和WQR0.5的检验统计量的经验水平分别为0.04和0.02；当误差分布服从t分布时，基于WCQR5和WQR0.5的检验统计量的经验水平分别为0.05和0.02。

总的来说，基于WCQR5的检验统计量的经验水平比基于WQR0.5的检验统计量的经验水平更接近事先给定的0.05，故基于WCQR5的检验统计量可以更好的控制第一类错误。本章提出的基于Bootstrap的检验方法不仅可以有更高的功效区分原假设和备择假设，而且对误差分布有一定的稳健性。