给定τ（0＜τ＜1），考虑下列的变系数分位数回归模型：

其中Y是反应变量，X∈Rp，α0τ（U），ατ（U）=（α1τ（U），…，αpτ（U））T是变量U的未知的函数，ετ是随机误差，给定条件（U，X），其τ分位数为0。模型（5.1.4）中Y的条件分位数回归模型为

假定｛Ui，Xi，Yi，i=1，…，N｝是来自模型（5.1.4）的独立同分布的样本，在没有截断的情况下，模型（5.1.5）中α0τ（·），ατ（·）的分位数估计量是下列函数的最小值

它的积分形式为

其中是｛Ui，Xi，Yi，i=1，…，N｝的经验分布。

在左截断情况下，我们用Fn（u，x，y）替代（5.1.6）中的，得

于是，通过使下列加权的分位数损失函数取最小值，我们获得模型（5.1.5）在左截断数据下α0τ（·），ατ（·）的加权分位数估计量

注意到（5.1.8）包含了未知的非参数部分α0τ（·）和ατ（·），这可由局部线性方法估计。具体地，当U接近u时，αjτ（U）（j=0，1，…，p）可局部线性近似为

αjτ（U）≈αjτ（u）+αjτ（u）（U-u）∶=ajτ+bjτ（U-u）。

则（5.1.5）可表示为

其中aτ=（a1τ，…，apτ）T，bτ=（b1τ，…，bpτ）T。

令是下列局部加权分位数损失函数的最小值(www.daowen.com)

其中Kh（·）=K（·/h）/h，K（·）是核函数，h是窗宽。则，。

为了方便起见，令和分别表示误差ε的条件分布函数和条件密度函数，fU（u）是U的边际密度函数。核函数K（·）是对称的密度函数，记

μj=∫ujK（u）du，νj=∫ujK2（u）du，j=0，1，2，…。

为了得到提出的估计量的极限分布，我们添加一些常规的条件。定义B（u）=。

（C1）F和G是连续函数且aG≤aF；

（C2）随机变量U有有界的紧支撑U，它的密度函数fU（·）是正的且对所有的u∈U，有连续的二阶导数；

（C3）核函数K（·）是对称的密度函数，具有有界的紧支撑且满足一阶Lipschitz条件；

（C4）当u∈U时，αj（u）是二次连续可微的，j=0，1，…，p；

（C5）对所有的u∈U，B（u）非奇异的，有连续且一致有界的导数且满足≥c0＞0。

对于分位数回归和变系数模型，这些条件一般被视为普遍的。特别地，条件（C1），保证了观察的数据依概率1没有结且系数是可识别的。条件（C1）与文献Zhou（2011）中的条件（C2）一样，条件（C2）—（C5）见Kai等人（2011）。具体地，条件（C2）和（C5）确保B（u）是可逆的且要求密度函数光滑。条件（C3）是包括Epanechnikov核在内的核函数的常规的条件。条件（C4）对局部线性估计量来说是必需的，因为αj（u）的二阶导影响偏差。

定理5.1.1　假定条件（C1）—（C5）成立。当n→∞时，若h→0且nh→∞，则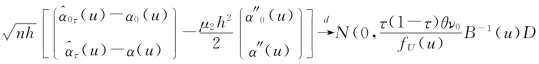（u）B-1（u）），其中D（u）=。