主要结果的证明-不完全数据下半参数回归模型的统计推

在证明定理之前，首先列出一些常规的条件。这些条件也被文献Zhou（2011）和Kai等人（2011）使用过。令δn=。

（C1）核函数K（·）是一个对称且连续的密度函数，具有有界的紧支撑，满足一阶Lipschitz条件，且＜∞，＜∞，j=0，1，2。

（C2）F，G是连续函数且aG≤aF。

（C3）随机变量W具有有界的支撑W，它的密度函数fW（·）是正的且具有二阶导数。

（C4）对所有的（X，W），Fε（0｜X，W）=τ，fε（·｜X，W）有连续且一致有界的导数且满足fε（·｜X，W）≥c0＞0。

（C5）对所有的w∈W，矩阵C2（w）和A是非奇异的。

（C6）函数g（·）有连续且有界的二阶导数。

引理4.4.1　令（X1，Y1），…，（Xn，Yn）是独立同分布的随机向量。假定＜∞且有＜∞，其中f（·，·）表示（X，Y）的联合密度函数。Kh（·）=K（·/h）是有界正函数且有紧支撑，满足一阶Lipschitz条件，则

只需要n2ε-1h→∞，其中ε＜1-s-1。

引理4.4.1由Mack和Silverman（1982）的结果可得。

引理4.4.2（Lv等人（2014））　假定An（s）是凸函数且可以表示为，其中V对称正定矩阵，Un是随机有界变量，Cn是任意的，对每一个s，rn（s）依概率收敛到0。则An的最小值αn 和+Cn的最小值βn=-V-1Un只相差op（1）。若同时有，则有-V-1U。

在下面的证明中，将用到一些随机向量的相关理论和方法。这方面已有丰富的结果，可参见文献Chen等人（2018），陈振龙和肖益民（2019）等。

定理4.1.1的证明　对给定w，则使下式取最小值

记

则是下列式子的最小值

由Kai（2011）中的式子（7.2），即

其中ψτ（u）=τ-I（u≤0），可得

接下来，证明E[Q2n（ξ）]=。

记，Δ和是中的Xi，Wi替换为x，w所得。由于是核形式的独立同分布随机变量的和，根据引理4.4.1，有

的期望为：

类似地，可获得=o（1），则+Op（δn），其中C1（w）=E[fε（0｜X，W）（1，（W-w）/h，XT）T（1，（W-w）/h，XT）｜W=w]。进一步，根据文献Liang和Baek（2016）的引理5.2，有

通过计算，有

因此

根据引理4.4.2，Qn（ξ）的最小值可表示为

因此

其中

接下来，考虑Q1n，1。记，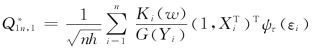

由Cramér-Wald定理和中心极限定理，有

定义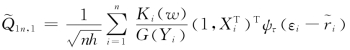，有

因此

由Slutsky定理，在给定X，W的条件下，有(https://www.daowen.com)

注意到

类似于（4.4.2）的证明，有Q1n，1-=op（1）。因此，

接下来计算的均值。

结合（4.4.4），（4.4.5），（4.4.6），（4.4.7）和（4.4.8），定理4.1.1得证。

定理4.1.2的证明　给定，则

记ri=-gτ（Wi），γ=，。则是下式的最小值

由Knight（1998），有

于是（4.4.9）可表示为

首先考虑V2n（γ）。记

的条件期望

通过计算，有

因此

记-E*（V2n（γ）｜X，W），易得=op（1）。注意到V2n（γ）=+op（1），则有

接下来，考虑V1n。定义。根据式（4.4.1），有

因此

由式（4.4.3），

其中δ（Xi，Wi）=。因此

观察到An=EAn+op（1）=+op（1）：=+op（1），因此

根据引理4.4.2，有

于是根据Cramér-Wald定理和中心极限定理，可得

其中B=E｛X-δ（X，W）｝⊗2。结合（4.4.11）和（4.4.12），定理4.1.2得证。

定理4.1.3的证明　的渐近正态性的证明与定理4.1.1的证明思路类似，这里省略。

定理4.1.4的证明　记，ri=-gτ（Wi），则是下列惩罚函数的最小值

使（4.4.13）取最小值等于使下式取最小值

上面的第二项可表达为

因此，可得。

记Bn，11是Bn左上角的s×s子矩阵。由于是Ln（ζ）的最小值且Ln（ζ）可被渐近的表示为

注意到Ln（ζ）是ζ的凸函数且L（ζ1）有唯一的最小值，由Geyer （1994）的特征值理论可得

则渐近正态性部分得证。

为了证明稀疏性，我们仅需要证明=0依概率趋于1。这等同于证明：若βτj=0，则→0。注意到≤max（τ，1-τ）＜1，若≠0，则我们有。因此，，结合→∞，可得→0。