在这一节，将通过模拟研究来评价提出的估计量和变量选择方法在有限样本下的表现。核函数为K（u）=0.75（1-u2）+。假定N=300是固定的，可观察的样本容量n是随机的。（同理，也可固定n且容许N是随机的。）另外，每一个模拟研究重复次数为100。在左截断数据下，F和G的乘积限估计量依赖Cn（·），以及随机截断的性质，Cn（y）可能趋于0，在有限样本下可能导致Fn（y）和Gn（t）的估计量不合理。因此，本章提出的分位数估计量可能受到影响。在模拟中，用

替代模型（4.1.2）中的Cn（y），可解决这个问题。

例1　考虑下列的部分线性分位数回归模型：

Y=X1β1+X2β2+g（W）+ετ，

其中Xi（i=1，2）由均值为1，两两协方差如下的多元正态分布产生：

W～U（0，1），β1=1，β2=2，g（w）=2+sin（2πw），ετ～N（-Φ-1（τ），1），它的τ分位数是0，Φ（·）是标准正态分布函数。截断变量T由均值为λ0的指数分布产生。不同的λ0对应不同的截断水平：

（i）当τ=0.25时，λ0分别取1.50，2.60，3.90，对应的截断率大约为10%，20%和30%；

（ii）当τ=0.50时，λ0分别取1.05，2.15，3.30，对应的截断率大约为10%，20%和30%；

（iii）当τ=0.75时，λ0分别取0.65，1.60，2.60，对应的截断率大约为10%，20%和30%。

为了评价本章提出的估计量（记作New）的表现，下面把它和omniscient估计量，naive估计量进行比较。Omniscient估计量是用全部的数据拟合分位数回归获得（样本容量为N）；Naive估计量则是完全忽略截断且运用截断数据下分位数回归获得（样本容量为n）。这里，运用一个简单的经验法则来确定窗宽，即omniscient估计量中的窗宽取N-1/5，本章提出的估计量和naive估计量中的窗宽取n-1/5。

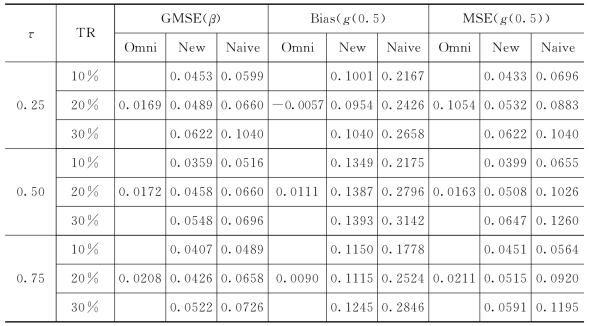
表4-1在三种不同的截断率下，基于omniscient方法，本章的方法和naive方法，给出了广义均方误差（Generalized Mean Square Error，记作GMSE），其中广义均方误差的定义为。同时，表4-1也给出了在三种不同的截断率下，g（0.5）的三种估计量的偏倚（记作Bias）和均方误差（mean square error，记作MSE）。另外，β1的三种估计量的箱线图，g（0.5）在τ=0.5，λ0=2.15（TR=80%）和4.65（TR=60%）下的QQ图见图4-1—4-2。

由表4-1，可得出如下结论。首先，omniscient估计量的表现最好，本章提出的估计量，它产生的偏倚和均方误差比naive估计量的小。其次，随着截断率的增加，本章提出的估计量和naive估计量的均方误差都变大。

图4-1—4-2表明：当截断率固定时，omniscient估计量的表现最好，而naive的表现最差。除此以外，随着截断率的增加，本章提出的估计量和naive估计量的表现越差。图4-2表明这三个估计量和正态分布拟合的很好。

表4-1　omniscient估计量，我们提出的估计量和naive估计量的比较

进一步，为了把我们提出的估计量与最小二乘估计量进行比较，我们考虑τ=0.5时ετ的三种误差分布：N（0，1）；t（3）和0.9N（0，4）+0.1N（0，100）。参数λ0分别为：

（a）对标准正态分布N（0，1），λ0的取值和上面的情形（ii）一致；

（b）对分布t（3），λ0分别取0.9，2.1，3.1，对应的截断率大约为10%，20%和30%；(www.daowen.com)

（c）混合正态分布0.9N（0，4）+0.1N（0，100），λ0分别取0.4，1.7，3.0，对应的截断率大约为10%，20%和30%。

基于最小二乘估计量，omniscient估计量，本章提出的估计量，naive估计量，β的广义均方误差GMSE和g（0.5）的均方误差MSE的结果见表4-2。其中，β的最小二乘估计量

表4-2　LS估计量，omniscient估计量，我们提出的估计量和naive估计量的比较，τ=0.5

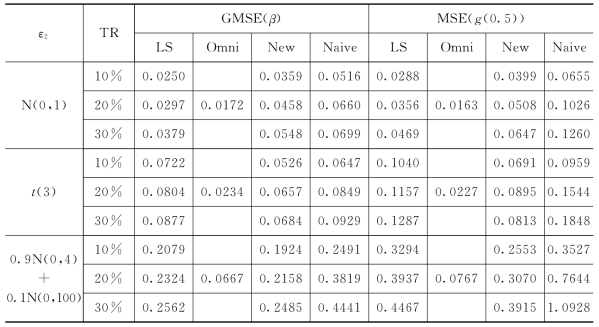
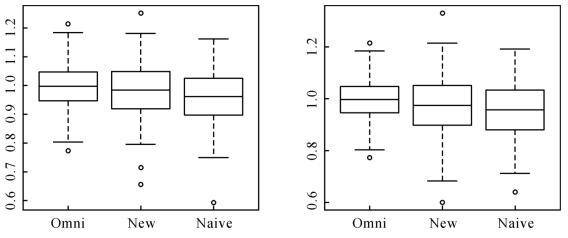
图4-1　β1的三种估计量的箱线图，TR=80%（左）和60%（右）

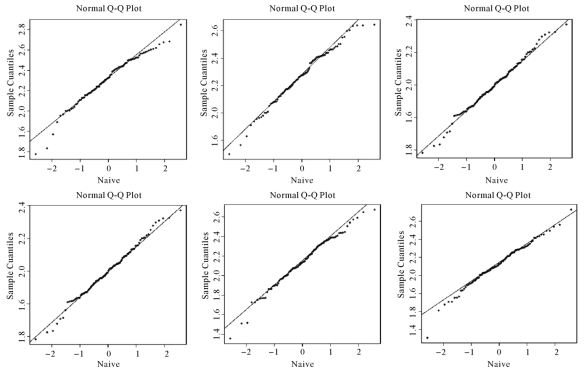
图4-2　g（0.5）基于Omni（左）方法，我们提出的方法（中）和Naive（右）方法，TR=80%（上面）和60%（下面）的QQ图

和基于的g（·）的局部线性估计量定义如下：

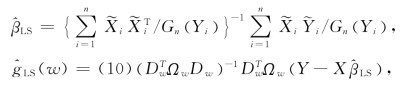
其中Ωw=diag｛Kh（W1-w）/Gn（Y1），…，Kh（Wn-w）/Gn（Yn）｝，Y=（Y1，…，Yn）T，

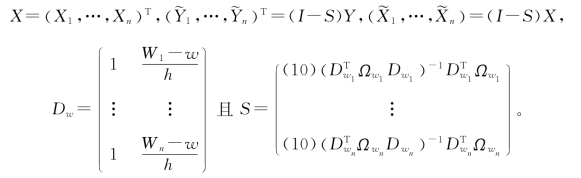
表4-2表明：当误差服从标准正态分布时，最小二乘估计量比本章提出的估计量的表现稍微好一点。然而，当误差服从其它分布时，本章提出的估计量比最小二乘估计量好，最小二乘估计量的表现比naive估计量好。潜在的原因是最小二乘估计量对异常值比较敏感，而分位数方法在大多数情况下比较稳健。

接下来，为了展示本章提出的变量选择方法的表现，做了如下模拟。

例2　在本例中，β=（1.5，0.5，0，1，0，0，0，0）T，Xi由均值为1，两两方差如式（4.2.1）的8维正态分布产生。其他和例1一样。

为了评价本章提出的变量选择方法，将把它和omniscient方法以及naive方法进行比较。广义均方误差被用来评价参数部分的变量选择方法的表现，模拟结果见表4-3。在表4-3中，‘C’代表非零系数被正确估计为非零的平均个数，‘IC’代表零系数被错误地估计为非零的平均个数。‘U-fit’（under-fit）代表剔除重要变量的模拟次数所占的比例；‘C-fit’（correct-fit）代表正确识别了重要变量且剔除无关变量的模拟次数所占的比例；‘O-fit’（over-fit）代表正确识别了重要变量但同时误挑选了无关变量的模拟次数所占的比例。

表4-3表明，通过比较广义均方误差（GMSE），可以发现，基于omniscient方法的变量选择方法表现最好，而naive方法最差。在所有情形下，本章提出的变量选择过程可以选出三个非零变量。其次，随着截断率的增加，本章提出的方法，其广义均方误差会变大，‘IC’和‘O-fit’变大而‘C-fit’变小。随着截断率的减小，‘C’越接近真实的非零系数的个数。这些结果表明：本章提出的变量选择方法，其模型选择结果是令人满意的。通过和真实的非零系数的个数进行比较，可以发现本章提出的变量选择方法，选出的模型非常接近于真实的模型。

表4-3　基于SCAD惩罚的部分线性模型的分位数回归的变量选择结果