在证明定理之前，先列出一些常规的条件，这些条件已被Zheng（1996），Fan等人（2013）和Niu等人（2016）使用过。

（C1）K（u）是对称的概率密度函数，有紧支撑。窗宽h满足nh3/2→∞且h→0。

（C2）G（·，θ），g1（·）和g2（·）满足一阶Lipschitz条件。

（C3）变量T有一个有界的支撑T，它的密度函数p（t）有连续的二阶导数且0＜c1≤p（t）≤c2＜∞。

（C4）Δt（t）几乎处处具有有界的二阶导数且inftΔt（t）＞0。

（C5）sup E（ε4｜X=x，T=t）＜∞，E‖X‖4＜∞且E‖η‖4＜∞。

（C6）Γ=E[Δ（X，T）（X-g1（T））（X-g1（T））T]是正定矩阵。

（C7）测量误差η独立同分布，其均值为0，协方差阵Ση已知，且与（X，T，ε）独立。

（C8）反应变量Y是随机缺失的，即在给定W和T的条件下，δ与Y条件独立。

引理3.3.1　（Zheng（1996）；引理3.2）设是独立同分布的随机变量序列，Hn（zi，zj）是一个对称的函数，且有

假设E[Hn（z1，z2）｜z1]=0，a.s.且对每一个n，＜∞。若

则当n→∞时，。

引理3.3.2　假设条件（C1）—（C6）成立。则当n→∞，有

证明　由wi的定义，可得

由Markov's不等式，可得0，且。引理3.3.2得证。

引理3.3.3　若条件（C1）—（C6）成立，则

证明　在原假设下，易得

类似地，在备择假设下，有

因此，引理3.3.3可证。

引理3.3.4　（Niu et al.，2016）在条件（C1）—（C6）和原假设（3.0.3）下，有

其中U可以是X或T，M（·）是连续可微的，‖M（·）‖≤b（·）且E｛b2（·）｝＜∞。

引理3.3.5　若条件（C1）—（C6）成立，则在原假设（3.0.3）下

在局部备择假设（3.1.9）下

其中θ0是θ的真值，G′（T，θ0）=∂G（T，θ0）/∂θ且Γ1=E｛G′（T，θ0）G′（T，θ0）T｝。

证明　基于（3.1.4），可得

根据Γ1的定义，可推出

在原假设下，

对In1变形，可得

注意到。

结合Xu等人（2012）中引理2的证明方法，有(www.daowen.com)

其中

类似的，In12=。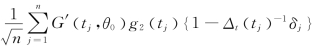

由上述结果可得

局部备择假设下的证明是类似的，这里略去。引理3.3.5得证。

定理3.1.1的证明　在原假设下，且注意到，Vn可被分解为

Vn1可写作U统计量的形式

其中zi=（δi，yi，，ti），i=1，…，n。｛zi｝是独立同分布的样本。在原假设下，由于E[Hn（z1，z2）｜z1]=0，Vn1是一个退化的统计量。类似于Zheng（1996）中的引理3.3a的证明过程，可得

对Vn2，有

引理3.3.3和引理3.3.4表明：且Vn21=。因此，可得

与文献Liang等人（1999）中的引理A.6类似，有

因此，可得

对Vn4，有

其中在与θ0之间。由引理3.3.4和3.3.5，可得

类似，易得=op（1），k=5，…，10。基于上述结果，可推出

基于U统计量理论，接下来证明的相合性。由的定义和（3.3.2）—（3.3.5）及引理3.3.1，可得

由条件（C1）和（C5），可推出

根据U统计量理论和引理3.3.1，可得

同理可证Ln的渐近性，定理3.1.1得证。

定理3.1.2的证明　在局部备择假设（3.1.9）下，且注意到ei=anH（ti）+ξi，Vn可被分解为

对Sn1，它可被分为

类似（3.3.2），可得。

由引理3.3.4，我们发现Sn1，2=且Sn1，3=+op（1）。因此，当an=，有

其中μ1，1=。对Sn2，我们有

由引理3.3.4，发现Sn2，1=Op（1），Sn2，2=，Sn2，3=。与文献Liang等人（1999）中的引理A.6的证明类似，可推出

于是由引理3.3.3，当an=，可得

由引理3.3.5，在备择假设下，可得[G′（T，θ0）H（T）]。因此，

对Sn3，在局部备择假设下，通过一些计算，可得

其中和在和θ0之间。根据引理3.3.4，可得Sn3，1=Op（1），Sn3，2=，Sn3，3=Op（1），Sn3，4=，Sn3，6=G′（T，θ0）G′（T，θ0）T｝。与文献Liang等人（1999）中的引理A.6的证明类似，可得Sn3，5=。于是，在局部备择假设下，可得

因此，结合（3.3.6）—（3.3.9），在局部备择假设（3.1.9）下，我们有。Ln的渐近性类似可得，定理3.1.2得证。