在这一节，把提出的检验方法应用到AIDS Clinical Trials Group（ACTG）175研究中。数据来源于R包“speff2trial”，包含了2139个阳性病人。关于这个数据集的详细的描述参见Hammer等人（1996）。记cd496表示96±5周的CD4数，cd40表示真实的CD4数，cd80表示真实的CD8数，wtkg表示体重（单位：千克）。我们感兴趣的是cd496，cd40，cd80和wtkg之间的关系。令Y表示cd496，X=（cd40，cd80）T，T=wtkg。将Y，X和T的值除以100来降低数量级。由于死亡和溺水，有37.26%的病人，其Y值是缺失的。正如Hu和Follmann（2010）一样，在该例中也假定Y是随机缺失的。另外，正如Huang和Wang（2000，2001）和Yang等人（2015）一样，cd40的数值会受到测量误差以及生物昼夜波动的影响。因此，在本节中，假定cd40和cd80有测量误差。

为了分析这组数据，可采用部分线性测量误差模型（3.0.2）来拟合这组数据。由于886个抗逆转录治疗的病人，他们的cd40和cd80被重复测量，利用这组数据，基于注3.1.1中的（c），可估计X的测量误差的协方差阵为=diag（0.8736，5.4251）。接下来的目的就是调查g（T）是否是某一线性形式。因此，运用提出的检验统计量来检验

H0：g（T）=θT，对某一θ=θ0 vs H1：g（T）≠θT，对任意θ。

核函数采用模型（3.2.1）中的核函数，窗宽为=0.0412。由（3.1.2），得到β的估计量=（2.8286，-0.1954）T。于是g（·）的非参数估计量为（见文献Sun等人（2009）），的图形见图3-2。(www.daowen.com)

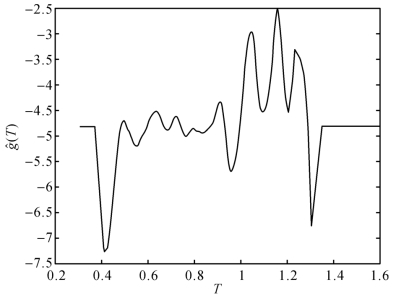
图3-2　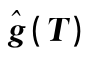的拟合曲线

检验统计量Vn和Ln的p值都是0，这表明应该拒绝g（T）的线性假设。进一步，由图3-2可得，显然不是T的一个线性函数。