例1　数据来自下面的部分线性测量误差模型

其中β=（β1，β2）T=（2，3）T，θ=1，Ti～U（0，1），Xi～N（（μ，μ）T，I2），其中μ分别是0，0.5和1，且I2是2×2单位阵，εi～N（0，1）。测量误差ηi～N（（0，0）T，Ση），取Ση=0.25I2和0.5I2来代表测量误差不同的水平。核函数是bi-weight核K（u）=，若≤1，反之为0。对模型（3.2.1），原假设H0：g（T）=θ｛exp（T）+cos（2πT）｝显然，a=0对应原假设；a≠0对应备择假设。在假设检验问题中，最优窗宽的选择正如Zhu和Ng（2003）提到的，仍然是一个开放性的问题，需要进一步的研究。为了调查本章的检验对窗宽的选择是否敏感，在接下来的模拟中试了2个窗宽：h0=和h1=，其中是T的样本标准差。每一个模拟重复1000次。

假设反应变量Y是随机缺失的，反应变量的示性变量δ服从Bernoulli分布，概率为Δ（W，T）。选择的三种缺失机制如下

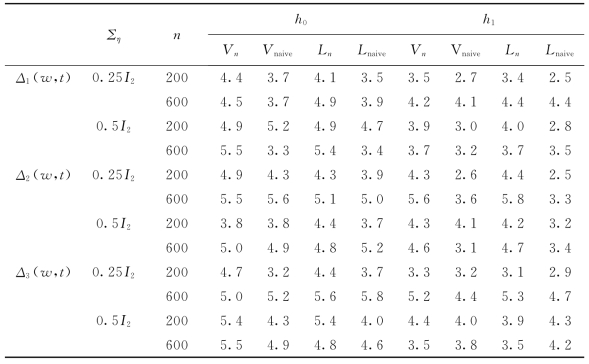
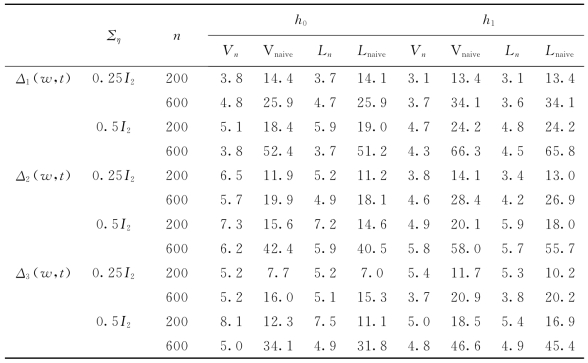
和上述三种缺失机制对应的平均缺失率分别近似为0.10，0.27和0.40。首先，我们研究检验统计量在三种缺失机制下的经验水平，给定显著性水平α=0.05，样本容量分别为n=200和600。为了评价我们提出的方法，把我们提出的检验统计量Vn和Ln和直接忽略测量误差且用W替代X的naive检验统计量进行比较。模拟结果见表格3-1—3-3（不同的窗宽和μ）。

从表3-1—表3-3，有如下发现：

（1）在以下模拟中，本章提出的检验统计量Vn和Ln几乎比naive检验统计量的表现好，因为提出的检验方法更接近预先指定的显著性水平0.05。

（2）当μ变大时，naive检验统计量很快就变差，而本章提出的方法是稳健的，因此本章提出的检验统计量可以很好地控制犯第一类错误的概率。

（3）当测量误差的方差越小或缺失率越小，本章提出的检验统计量的表现越好。

（4）在相同的缺失机制，样本容量和测量误差下，本章提出的检验方法在不同的窗宽下有类似的结果。

（5）对模型（3.2.1），Vn和Ln有类似的结果。

表3-1　不同缺失机制和窗宽下经验的检验水平（×10-2），μ=0

(www.daowen.com)

表3-2　不同缺失机制和窗宽下经验的检验水平（×10-2），μ=0.5

接下来，借助功效来展示测量误差、缺失机制、窗宽和μ对检验统计量产生的影响。在模型（3.2.1）中，取a=0∶0.3∶3。给定水平a=0.05，n=100，模拟次数1000次，先计算检验统计量经验的检验水平和检验功效。进一步，用图形来展示结果，给出了n=100和水平α=0.05下的经验的检验水平和检验功效。表3-4仅给出了Ση=0.25I 2和缺失机制Δ1（w，t）下的结果，图3-1给出了窗宽为h0和μ=0下的功效曲线。其他情况下的结果类似。

表3-3　不同缺失机制和窗宽下经验的检验水平（×10-2），μ=1

表3-4　在Δ1（w，t）下，不同窗宽和μ下检验统计量经验的检验水平（×10-2）和检验功效（×10-2）

续表

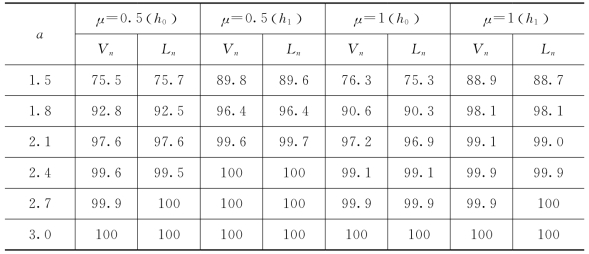
由表3-4，可以发现：随着a的增加，检验统计量的功效也快速的增加。这说明本章提出的检验方法可有效的识别出备择假设。进一步，检验统计量的功效对不同的窗宽不敏感。图3-1也表明本章提出的方法不仅可以有很高的功效区别原假设和备择假设，而且对测量误差具有一定的稳健性。另一方面，在α≠0时的备择假设下，基于上述三种缺失机制，测量误差越小，对应的功效越大。再者，在相同的测量误差下，缺失的数据越少，本章提出的检验方法越好。

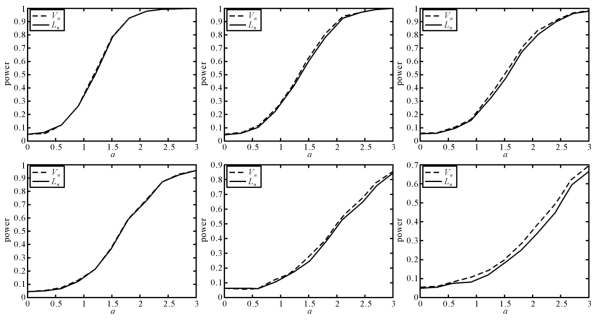
图3-1　两个检验统计量的功效曲线，缺失机制分别为：Δ1（w，t）（左），Δ2（w，t）（中），Δ3（w，t）（右）且Ση=0.25I2（上面），Ση=0.5I2（下面）