在这一节，我们利用模拟研究来评价经验似然比检验统计量在有限样本下的表现。

例1　考虑如下的回归模型

其中ε～N（0，0.42）。变量X分别来自正态分布N（1，1），均匀分布U（0，2）和指数分布Exp（1/4）+3/4。取高斯核K（x）=exp（-x2/2）/作为核函数K（x）。L（x）=是bi-weight核函数，其中I（·）是示性函数。窗宽hCV可通过交叉验证的方法获得，即使得下面的式子取得最小值，

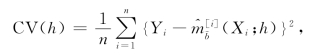
其中是m（·）的估计量，它是由去除第i组样本的观测值计算而得，=n-1/8。我们可用同样的方法选择窗宽a。p（x）=P（δ==x）是选择概率函数，考虑如下三种随机缺失机制

（1）p1（x）=0.8+如果≤1，反之为0.95；

（2）p2（）x=0.9-如果≤4.5，反之为0.1；

（3）p3（）x=0.6对所有的x。

当X～N（1，1），上面三种情况的平均缺失率分别是9%，26%，40%左右。当X～U（0，2），上面三种情况的平均缺失率分别是10%，20%，40%左右。当X～Exp（1/4）+3/4，上面三种情况的平均缺失率分别是5%，25%，40%左右。关于X的辅助信息是E（X）=1。

首先，在上面三种情况下，研究检验统计量T01犯第一类错误的概率。为了评价我们提出的方法，以下把我们提出的方法（记作our EL）和不带约束条件的检验统计量T02对应的方法（记作“naive EL”），仅用观测到的数据的方法（记作CDM），在没有使用辅助信息下，我们提出的方法（记作no AI）进行比较。对每一个选择概率函数p（x），考虑三种分布，即N（1，1），U（0，2），Exp（1/4）+3/4且θ0=2。给定显著性水平α=0.05，每一个模拟重复1000次。约束条件是θ≥2。样本容量n分别为100和300。模拟结果见表2-1。进一步，为了展示模型误差的影响，我们给出了检验统计量T01在三种不同的模型误差下犯第一类错误的概率。这三种模型误差分别是t（2），t（3）和t（5）。选择概率函数是p2（x），n=300，α=0.05，模拟次数为1000次，模拟结果见表2-2。

其次，我们利用检验统计量的功效来比较我们提出的检验方法、CDM方法和no AI方法。考虑模型（2.3.1），对每一个给定的τ，X～N（1+τ，1）。其他的变量和模型（2.3.1）中的一样。检验H0：θ=2 vs H1-H0：θ＞2，我们取τ=0：0.05：1；对检验H1：θ≥2 vs H2-H1：θ＜2，我们取τ=-0.5：0.05：0.3。图2-1、图2-2分别是T01和T12在缺失机制p1（x）和p3（x）下的功效曲线，样本容量分别是n=100和200，α=0.05，模拟次数为500次。

最后，为了展示双边假设检验中T34和T24在“our EL”，“CDM"和”“no AI”方法下的表现，我们考虑模型：Y=X+ε，ε～N（0，1），X～N（τ，1）。图2-3给出了检验统计量T34在检验H3：θ=-0.8或0.8vs H4-H3：-0.8＜θ＜0.8中的功效曲线。图2-4给出了检验统计量T24在检验H4：-0.5≤θ≤0.5 vs H2-H4：θ＜-0.5或θ＞0.5中的功效曲线。图2-3和图2-4中的缺失机制是p1（x）和p3（x），n=100和200，α=0.05，模拟次数为500次。

表2-1　不同缺失机制下的犯第一类错误的概率，α=0.05

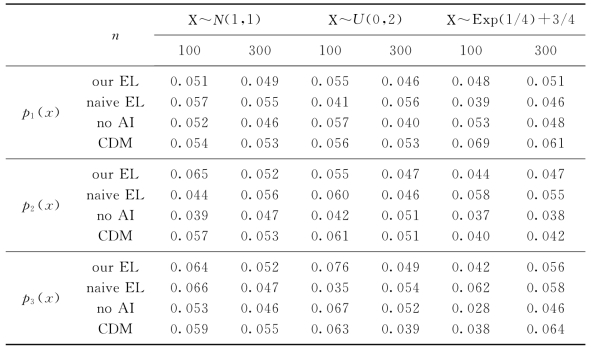
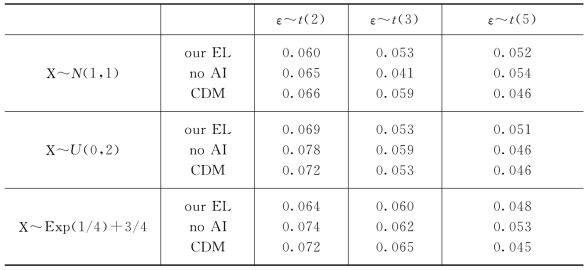
表2-2　犯第一类错误的概率：缺失机制为p2（x），α=0.05，n=300

(www.daowen.com)

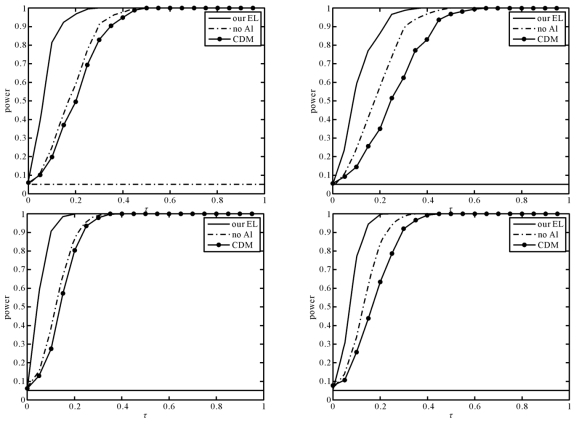
图2-1　T01在p1（x）（左边）和p3（x）（右边）下的功效曲线，n=100（上面）和200（下面）

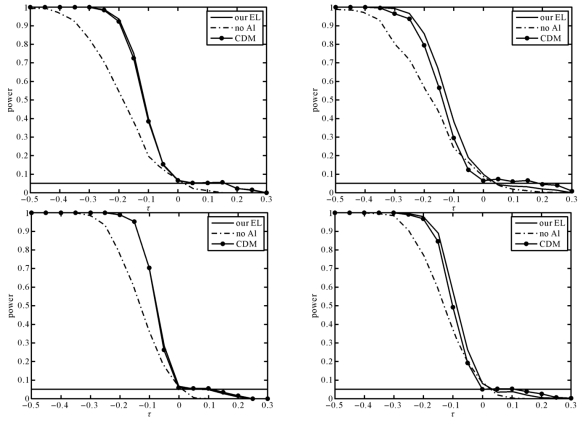
图2-2　T12在p1（x）（左边）和p3（x）（右边）下的功效曲线，n=100（上面）和200（下面）

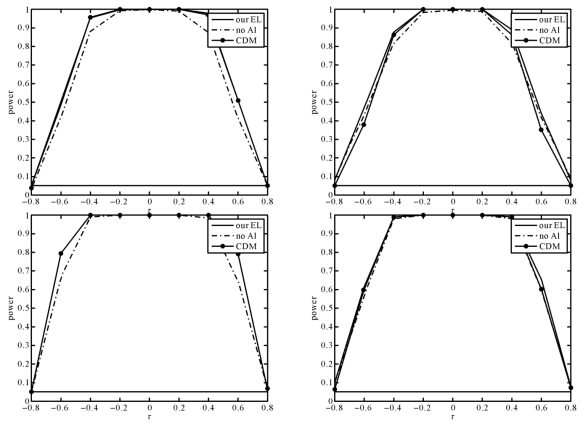
图2-3　T34在p1（x）（左边）和p3（x）（右边）下的功效曲线，n=100（上面）和200（下面）

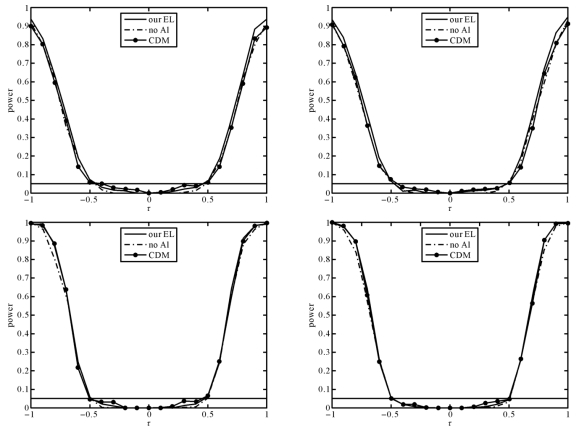
图2-4　T24在p1（x）（左边）和p3（x）（右边）下的功效曲线，n=100（上面）和200（下面）

从表2-1—2-2和图2-1—2-4，我们可得如下结论：

（1）表2-1表明，在三种缺失机制下，随着样本容量n的增加，犯第一类错误的概率收敛到水平α。而且，我们提出的检验方法优于“naive EL”方法，“CDM”方法和“no AI”方法。原因是我们提出的方法使用了辅助信息，同时融入了纠偏加权的方法和不等式的约束条件。进一步，随着缺失率的增加，我们提出的方法和“no AI”方法优于“CDM”方法。

（2）当样本容量n相同且在相同的水平α下，表2-1将三种缺失机制进行了对比。p1（x）的平均缺失率最小，对应的表现最好。p3（x）的平均缺失率最大，对应的表现最差。

（3）在三种模型误差下，检验统计量T01的表现很好。而且，在模型误差服从t（5）分布时，和其他两种模型误差相比，检验统计量犯第一类错误的概率更接近水平α。当模型误差服从t（2）分布时，和其他两种模型误差相比，检验统计量犯第一类错误的概率离α更远。原因是在这三种分布t（2），t（3）和t（5）中，t（2）分布的尾概率最大，而t（5）分布的尾概率最小。

（4）从图2-1—2-4可以看出，在不同的缺失机制p（x）下，我们提出的方法比“CMD”和“no AI”方法好。同时，n=200时的功效比n=100时的功效好。

（5）在模拟中，τ=0时的T01和T12，τ=±0.8时的T34，以及τ=±0.5时的T24的备择假设都变成原假设，此时功效应该接近于α。因此错误的拒绝原假设的概率应该接近于α，这可以从图2-1—2-4中看到。

（6）图2-1表示随着τ增加，功效快速的增加。图2-2表示随着τ增加，功效快速的减少。图2-3表示当τ远离边界时，检验统计量倾向于拒绝原假设。图2-4表示-0.5和0.5是假设H4：-0.5≤θ≤0.5的临界点。图2-1—2-4表明，在不同的缺失机制下，检验统计量的表现非常稳定。这些显示我们的检验不仅可以以高的功效区分原假设和备择假设，同时对缺失率在一定程度上具有一定的稳健性。

因此，当反应变量缺失时，反应变量均值的上述假设检验问题建议采用我们提出的方法。