针对随机缺失机制模型，已有的完全数据的理论和方法无法直接应用。通常的方法是给每一个缺失的反应变量插补一个值，得到一组完全数据，再用标准的统计方法。借助核回归插补方法，Wang和Rao（2002）利用插补方法得到Y的完全数据集，其中

其中是m（x）=的截断版本的估计量，即

Kh（·）=K（·/h）是核函数，h∶=hn和b∶=bn分别是趋于0的正的常数序列，称之为窗宽。由于（2.1.1）包含一个插入的非参数估计量，由此可见存在偏倚-m（Xi）。为了减少偏倚，我们使用纠偏加权的插补方法，这种方法可被视为是Horvitz-Thompson逆概率加权方法和加权方法的联合，且已被很多学者使用过（见Robins等人（1994），Liang等人（2004），Xue（2009））。具体地，使用纠偏加权的，i=1，…，n作为Y的完全样本，定义如下

其中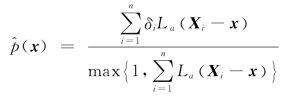是p（x）的估计量，La（·）=L（·/a），L（·）是核函数且a∶=an是窗宽。

根据Owen（1990），反应变量Y的均值θ的一个纠偏加权的经验似然函数定义为

借助Lagrange乘数法，由于pi=pi（θ）=，1≤i≤n时，（2.1.2）有最大值，其中λ=λ（θ）是方程=0的解。因此，忽略常数项-nlogn，我们定义θ的纠偏加权的经验对数似然比函数为(www.daowen.com)

在某些情况下，X的一些辅助信息是可获得的，即存在q（q≥1）个函数A1（x），…，Aq（x），使得

其中A（x）=（A1（x），…，Aq（x））T。例如，若E（X）的均值已知，取A（x）=X-E（X），可得式（2.1.3）；当X是1维随机变量，若X的分布关于一个已知的常数x0对称，取A（x）=I（X≥x0）-，则式（2.1.3）成立；给定区间（a，b），若已知P（a＜X＜b）=p0，则可取A（x）=I（a＜X＜b）-p0。为了使用式（2.1.3）中关于X的辅助信息，基于（2.1.3），我们提出带辅助信息的θ的纠偏加权的经验似然函数

其中ψi（θ）=（A（Xi）T，-θ）T。假设初始值在点ψ1（θ），…，ψn（θ）的凸包里面。借助Lagrange乘数法，（2.1.4）有最大值，其中

η=（η1，…，ηq+1）T是方程

的解。类似地，忽略常数项-nlogn，我们定义带辅助信息（2.1.3）的θ的纠偏加权的经验对数似然比函数如下