交换排序也叫冒泡排序。冒泡排序是按以下方法实现的。

假设待排序的数列有n个数，从第0个元素开始，将第0个元素逐一与后面的每一个元素（i=1～n-1）比较，如果第i个元素比第0个元素小，就将第i个与第0个元素进行交换；否则，保持原来的位置。这样经过一遍处理后，从第0个元素到最后一个元素中最小的那个数就“浮”到第0个元素的位置上。第2遍用同样的方法，将第1个元素与其后面的每一个元素（i=2～n-1）进行比较，最终将余下的数中最大的一个置换到第1个元素的位置上。如此反复，第i遍处理后，就将余下的最小元素交换到第i个元素的位置上。如图9-2所示，每轮交换完成后就将最小的数“浮”到上面。

以上方法进行排序得到的结果是升序数列，如果比较时将较大的数“浮”到第i个元素位置，得到的结果为降序排列。

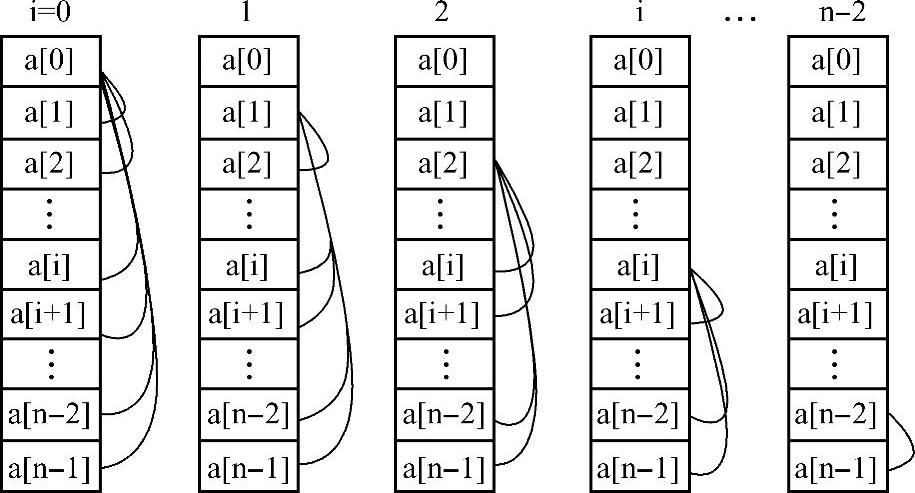
图9-2 交换排序算法1

另一种冒泡排序方法是对相邻的两个数进行比较：从第0个元素开始，对相邻的两个元素比较大小（第0个元素与第1个元素，第1个元素与第2个元素，……第i个元素与第i+1个元素，……第n-2个元素与第n-1个元素），如果小的在前，大的在后，保持原顺序；否则，这相邻的两个数进行交换，完成一遍处理（比较到第n-1个元素）后，最大数就“沉淀”到最后一个元素n-1的位置。第2遍用同样方法，再从第0个数处理到第n-2个数，将剩余的第0～n-2个元素中最大的那个数“沉淀”到第n-2个元素的位置。第i遍处理后，将余下部分中最大元素交换到第n-i-1位置上。如图9-3所示，每轮交换完成后就将最大数“沉淀”到本轮的最后面一个元素。

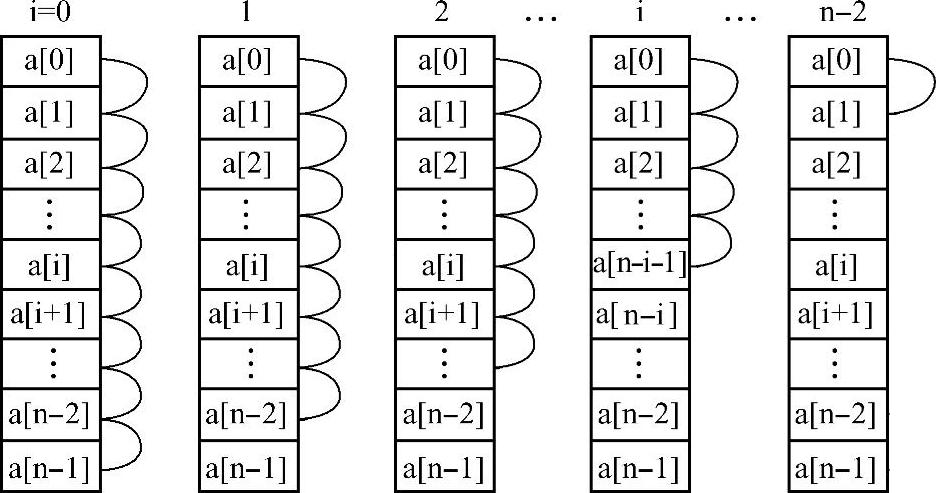
图9-3 交换排序算法2

【例9-19】冒泡算法1：将一个无序数组，按从小到大的顺序进行排列。(www.daowen.com)

程序思路：根据第一种方法，将第0～n-2位置上的数与其后的数进行比较。因此，程序需要两层循环，外循环计数变量为i，i的变化应该从0到n-2；内循环计数为j，完成第j个元素与外循环的第i个元素的比较，由于第j个数在第i个数后面，其位置从i+1直到n-1。所以内循环j计数从i+1到n-1。

程序运行结果：

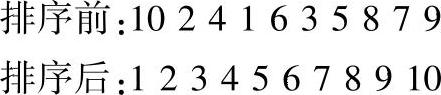
【例9-20】冒泡算法2：将一个无序数组，按从小到大的顺序进行排列。

程序思路：根据第二种方法，对相邻的两个数进行比较，程序同样需要两层循环。当数组有n个元素时，共需要n-1轮比较。设外循环计数变量为i，i的变化应该从0到n-1；第0轮比较时，两两相邻元素所需要的比较次数为n-1，第i轮比较时，参加比较的元素有n-i个，比较次数为n-i-1，因此内循环计数j应该从0到n-i-1，以完成第j个元素与相邻的第j+1个元素的比较。

程序运行结果：（略，结果同例9-19）