迭代法也称辗转法，是使用变量的旧值递推出新值的过程。迭代算法通过计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令（或这些步骤）时，都从变量的原值推出它的一个新值。迭代与递推在算法思想上基本是一致的。

使用迭代算法解决问题，需要注意以下3方面的内容。

1）确定迭代变量：在可以用迭代算法解决的问题中，至少存在一个直接或间接的不断由旧值递推出新值的变量，这个变量就是迭代变量。

2）建立迭代关系式：迭代关系式是指如何从变量的前一个值推出其下一个值的公式（或关系）。迭代关系式的建立是解决迭代问题的关键，通常可以使用顺推或逆推的方法来完成。

3）对迭代过程进行控制：在合适的时候结束迭代过程，不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，通过一个固定次数的循环来实现对迭代过程的控制；另一种是所需的迭代次数无法确定。需要根据问题要求，确定结束迭代过程的条件。

【例9-7】使用欧几里得迭代算法，求两个整数a，b的最大公约数。

程序思路：定理gcd（a，b）=gcd（b，a%b），即整数a，b的最大公约数与b，a%b最大公约数是相同的。欧几里得算法就是根据这个定理，进行辗转相除法。程序上反复进行迭代计算，直到余数等于0为止。

例如：27，15两个数，则有15，27%15→15，12→12，15%12→12，3→3，12%3→3，0；余数为0，得出最大公约数3。

程序运行结果：

3

【例9-8】使用迭代算法，求Faibonacci序列数的前12项。

程序思路：Faibonacci序列数，有f（i）=f（i-2）+f（i-1），第i项与第i-1项和第i-2项形成迭代关系。求出当前项x3=x2+x1，进入下一项后，用x1迭代前一项的x2，用x2迭代当前项的x3。迭代次数为12。

程序运行结果：

1 1 2 3 5 8 13 21 34 55 89 144(www.daowen.com)

下面介绍牛顿迭代法。

迭代法可以用来求解方程。这种方法通过对数值进行分析，先确定一个初始近似值作为预估的解，由此预估值出发继续迭代寻找更为近似的解来得到问题最终的解。这种方法一般用于解方程或者方程组，牛顿迭代法就是用于求方程或方程组近似根的一种常用的算法。

牛顿迭代公式为：。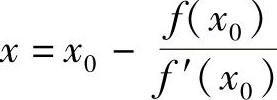

牛顿迭代法求解释方程f（x）=0的根的步骤是：

1）设一初值x0。

2）根据迭代公式x=x0-f（x0）/f′（x0）计算出下一个x。

3）用刚计算出的x取代上一个x0值，再用迭代公式计算新的x，直至两次计算出的x值的差的绝对值x-x0不超过指定的误差值e为止。

【例9-9】使用牛顿迭代法，计算2的平方根。要求精度为10^-10。

程序思路：求解2的平方根，可以设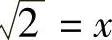，即x²-2=0，则方程为f（x）=x²-2；求f（x）的导数f′（x）=2x；

所以，迭代公式为x=x0-f（x0）/f′（x0）=1/2*（x0+2/x0）。

程序运行结果：

1.4142135623746899