在教学设计中应营造一个“再创造”的环境，引导学生通过对已有认知结构无法包容的新问题新现象进行分析、讨论、探索，在解决问题和发现规律中逐步实现知识与能力的增长，实现认知结构的同化与顺应。我们可将活动流程设计为“认知准备、以疑激探—分析问题、建构新知—变式再探、把握本质—应用实践、深化认识—回顾小结、反思悟化”。在这种教学方式下，学生成为自主探索的主体，亲身经历知识的发生发展过程、问题的解决与规律发现的过程，并深刻体会直观感知、观察发现、归纳类比、抽象概括、反思与建构等历程，其结果必然是一个问题导引、学生积极参与、师生有效交互、学生自主建构、理解不断加深的高效课堂。

案例：一节突出数学本质、深化概念理解的课例——几何概型的教学设计

1.认知准备、以疑激探

问题1：前面我们学习了古典概型，你能不能举一个用古典概型能够解决的生活中的问题？

问题2：是不是所有的随机试验都能用古典概型求事件发生的概率？你能举一个例子吗？

预案：如果学生所举的例子正好符合几何概型，就将其利用起来作为后续探究的问题源使用；如果没有，教师还可以补充如下例子。

问题3：（图12-7）大圆内有一个同心小圆，向圆形区域内投掷一飞镖，求飞镖落入小圆区域的概率。

问题4：校门口的红绿灯，红灯亮的时间为41秒，绿灯亮的时间为36秒，黄灯亮的时间为3秒，求当你到校门口时，恰好遇到红灯的概率。

设计意图：“提出问题比解决问题更重要。”因为解决问题是被动的，主动提出问题才是创造的，才能更好地发展学生的数学素养。此处设计，目的是让学生产生研究新问题的求知欲，激发学生生成智慧。

利用所举的例子进行探讨，如问题3。

问题5：这个问题的概率是多少？你是怎样得到的？这个计算公式是古典概型的计算公式吗？

问题6：这个例子不是古典概型，但是为什么可以用这么一个式子算出一个我们认为都正确的结论呢？古典概型的概率公式和这个计算在式子形式上有何关系？

预案：此处根据学生的回答相机而行，最重要的是要让学生发现古典概型公式中的分子和分母中的基本事件个数被几何度量（面积、长度等）所代替了。

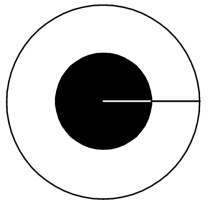
图12-7

然后老师追问：

①为什么可以进行这种替换？我们分析一个随机试验的概率问题首先考虑什么？

②这个问题中的基本事件是什么？

③为什么可以用面积（或长度）比得到这个概率呢？

……

设计意图：理解需要思考，这里通过追问，让学生利用类比的方法来分析解决新问题，实现由直观感知到初步理解的过渡，为后续概念教学铺好路。

2.总结共性、建构新知

问题7：在边长为2的正方形内有一个内切圆，向正方形内随机投一个点，分析该点落入圆内的概率是多少？(www.daowen.com)

此处老师引导学生一起解决问题，之后提出下列问题：解决这一问题的办法是什么？你能说出怎样的随机试验问题可用这样的办法解决吗？

设计意图：通过提问，让学生发现这类问题的本质特征：即基本事件具有“无限个”“等可能”的特征，可用几何测度之比求概率。此时可因势利导引出几何概型的概念、概率计算公式，实现新认知的建构。

3.变式再探、把握本质

图12-8

问题8：如图12-8所示的两个边长为2的正方形区域内各有一个面积为1的深色区域，现将一颗豆子随机地扔在正方形内，那么它落在桃形区域与椭圆形区域内的概率一样吗？为什么？（不计豆子的面积且豆子都能落在正方形区域内。）

问题9：①在区间[0，9]上任取一个整数，恰好取在区间[0，3]上的概率为多少？②在区间[0，9]上任取一个整数，恰好取在区间[0，3]上的概率为多少？

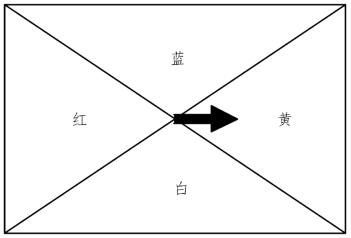
图12-9

问题10：如图12-9，将一个长与宽不等的长方形水平放置，长方形对角线将其分成四个区域。在四个区域内涂上红、蓝、黄、白四种颜色，并在中间装个指针，使其可以自由转动。对于指针停留的可能性，下列说法正确的是（　）。

A.一样大

B.黄、红区域大

C.蓝、白区域大

D.由指针转动圈数确定

设计意图：通过问题8，让学生明白几何概型的概率只与测度大小有关，与图形的形状无关；通过问题9，强化选用概型先看事件属性的意识；而问题10的设计非常好，造“陷阱”让学生误以为是直接用三角形的面积比，通过此题重点强调使用几何概型时一样要注意基本事件的“等可能性”，此时老师强调正确的几何度量应该是“角度”，而不是“面积”。上述系列问题，让学生体悟到，对于几何概型的学习，不仅要记住定义，更重要的是要把握它的本质属性。只有这样，才能用准用活概型解决问题，防范差错的出现。

4.应用实践、深化认识

问题11：某人午觉醒来，发现表停了，他打开收音机，想听电台报时，求他等待的时间不多于10分钟的概率。

预案：可将一个小时内的时间与分钟的转动联系起来，引导学生类比转盘中的面积、角度、弧长等来求概率，老师在课堂上留足时间让学生想，留给机会让学生说，展示不同层次学生的想法，并解释所选择几何度量的合理性。同时，老师还可引导他们将时间转化成长60的线段，用长度之比来求概率。

待学生展示解法之后，引导学生反思：①这个问题本身并不是几何问题，但却可以用几何概型一题多解，这是为什么？②你对几何概型的使用有何体会与认识？

设计意图：通过这个例题，让学生悟明白几何概型并不是只研究与几何有关的概率模型，实际上有的例子与几何没有直接的关系，而是可通过几何图形去合理地描述转化，求解问题的关键是要找出实际问题的本质，从而深化学生对几何概型的理解。

5.回顾小结、反思悟化

问题12：①几何概型的特点有哪些？②你认为几何概型与古典概型有哪些异同？准确使用概型的关键是什么？