在风险评估过程中,风险识别的对象是事物或活动,事物或活动经过范围界定后,危险只需评估人员根据特定方法一一寻找辨别即可;风险分析是将每一个风险点,按照分析方法进行定性、定量处理,而每个风险点均有无限损害发生的可能。众多风险评估方法中,每一种评估方法首要解决的问题是处理各种不确定性的问题,综合数据库法概莫能外。

综合数据库法下的危险-风险特性事件模型是根据事件发生的时序因果联系,利用情境分析的理论方法,构建出事件理论模型,通过科学严谨的描述而建立的。危险-风险特性事件模型是假设其他因素静止无影响,由某一类型因素影响的单一事件模型,企业风险评估人员会产生疑惑:每个事件都是单个因素影响的独立事件,没有在整个生产活动系统中考虑;每个事件都有自身特性,独立于其他事件,单一地描述典型事件,没有对全部事件、全部损害后果的统计;每个事件发生的暴露、可能性、后果性,这三种主要的要素分析仅在于理想状态下事件模型里,不具备实践指导意义;每位评估人员的经验技术水平、风险评估方法应用能力参差不齐,难以确保风险分析的可靠性、科学性,导致风险评价结果失真。

提炼安全风险评估人员在运用分析方法的过程中产生的各种疑问,我们发现分析方法归根结底要解释两个问题:各种不确定性划归于某些特定的确定性事件,能否囊括所有的不确定性的属性;某些确定性事件的结论是否于现实有实践意义。

根据风险的一般定义,风险既是各种可能性、不确定性（隐含着许多后果在内）。以顶板浮石不处理的事件举例,浮石产生的物质特性不确定,如硬度、形状（棱角）、质量等;浮石存在的高度不确定,如巷高、人员工作高度;人员在浮石下方活动的时间不确定;浮石冒落的可能性大小不确定;造成的后果,有人轻伤、重伤、无伤害（有人恰巧躲避）等等事件要素的不确定。综合数据库法的危险-风险模型就是将各种可能性（评估人员各种描述、取值等）均考虑进去,构成一种理论中发生的事件进行数据分析。

风险事件中的很多要素对事件终止结果都产生了或多或少的影响,为便于数据处理,只选用顶板浮石冒落的可能性来进行说明,见图5-5。

每个人依据自身经验,对浮石冒落的可能性有着不同的认识。假设所有评估人员均采用同样的评估方法,评价标准进行判断:甲依据自身经验判断,这种事件（事件中的某一环节）发生的概率很大,在描述中会表述成“可能”;乙依据自身经验判断,这种事件的可能性为“十分可能”;丙同样依据经验和评估方法,判定此事件的可能性为“很少的可能性,据说曾经发生过”。每位评估人员对事件可能性的判定都有自身的理由,且都没有超出大众对事物经验认知的范畴,所以每个人的评估结论都是合理的。

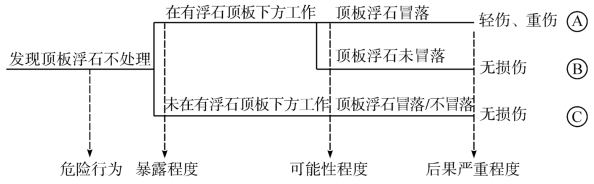
图5-5　风险事件的影响因素

我们将评估人员对顶板浮石冒落的可能性分析作为事件处理,记为事件A,其发生的概率为P,那么P（A）发生的概率肯定是1。因为我们已经将此事件的必然后果考虑完备了,哪怕是所有人都评估事件A没有发生的可能性,事实是事件A在评估开始已经发生,概率为1。

根据可能性评价表（见表5-15）,总计有6种事件结果,因为每个人对事件的判定经验不同,所以每个事件的发生概率并非是1/6。例如“相当少但却有可能,多年没有发生过”这个选项,根据经验,每位评估人员都不会选择的;“可能（25%）”,这个选项,每位评估人员都倾向于选择。

表5-15　可能性评价表

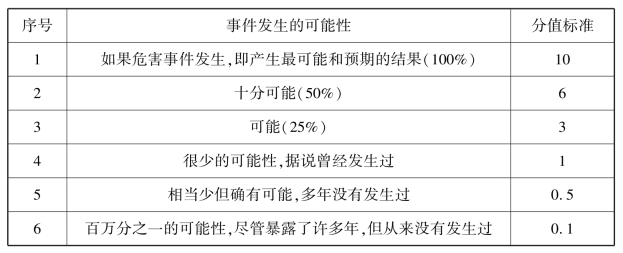
然后我们将每位评估分析人员对事件可能性的分析作为各种可能的后果事件进行分析,即为子事件a,依次排列为a1,a2,a3……a6。P（A）=p（a1）+p（a2）+p（a3）+……+p（a6）=1。

在某次企业风险评估过程中,召集生产技术科和机掘二队风险评估人员20人,对事件“发现顶板浮石不处理”事件进行5次风险特性分析,在分析之前,事件的危险特性分析、描述已完成,评估人员必须在此框架内完成对危险源的风险特性描述。每位成员依次描述,一轮完成后间隔一天后再次进行特性分析,当次的特性分析描述可以对上次的分析结果修改,最后由技术服务人员对评估数据做如下汇总,见表5-16。

表5-16　风险特性中可能性事件结论统计表

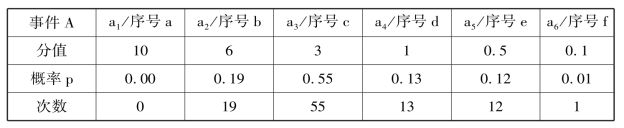
事件a2的概率等于导致事件a2的结果数量与所有可能结果总数之间的比值,p（a2）=19/0+19+55+13+12+1=0.19;评估人员认为顶板浮石掉落的可能性为“十分可能（50%）”的概率为0.19。同理,评估人员认为顶板浮石掉落的可能性“可能（25%）”的概率为0.55,依次类推。

我们将风险评估人员对可能性的取值进行统计,绘制了直方图:

通过图5-6,我们可以看出,大多数评估人员或同一评估人员更多地认为,顶板浮石发生的可能性为“可能（25%）”。

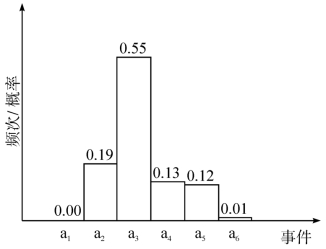
图5-6　可能性事件直方图

我们将可能性取值绘制成曲线图,可得到类似偏态分布图,见图5-7。

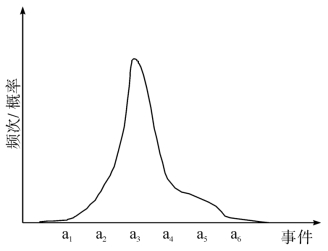
图5-7　可能性事件偏态分布图

按每个评估人员的分值进行统计学分析,建立离散型随机变量模型。(www.daowen.com)

有100次评估人员对A事件的可能性分值进行分析描述（打分）,所有人员的可能性结果A{0.5、0.1、10、6、3、1、0.5、0.1、0.5、0.5、10……}共计100个,做为an,计算所有分值的中心值（平均数）μ,

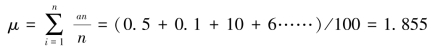
计算所有分值的方差σ2;

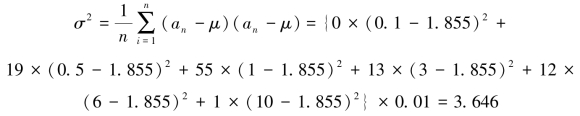
以上图像是服从正态分布记作N（μ,σ2）,μ=1.855,σ2=3.646。

正态分布曲线的面积是总概率值1。概率顶点说明大多数的评估人员取值在此处,两翼说明极小部分评估人员取值在此处。σ2越小,曲线越瘦高,说明大多数的意见一致;σ2越大,曲线越低矮,说明人员的意见不统一,成分散状态。经过多次评估后,大多数评估人员取值靠近顶点的位置,说明经验取值接近于实证科学,说明此项分析结果是绝大多数评估人员认可的,评估结果能准确反映该类型事件风险程度,事件模型具有指导实践的最大多数情况的意义。例如,中保研对测试车辆（只选取一辆）进行模块化的标准碰撞测试,来评定汽车某方面的性能,虽然用车环境、路况千变万化,确认对汽车使用者具有指导意义。对危险-风险事件模型进行概率统计分析,解释了典型的、单个事件的结论具有普遍的指导性意义。

对事件模型中其他要素的分析,其数据呈现如图5-8所示的偏态分布。

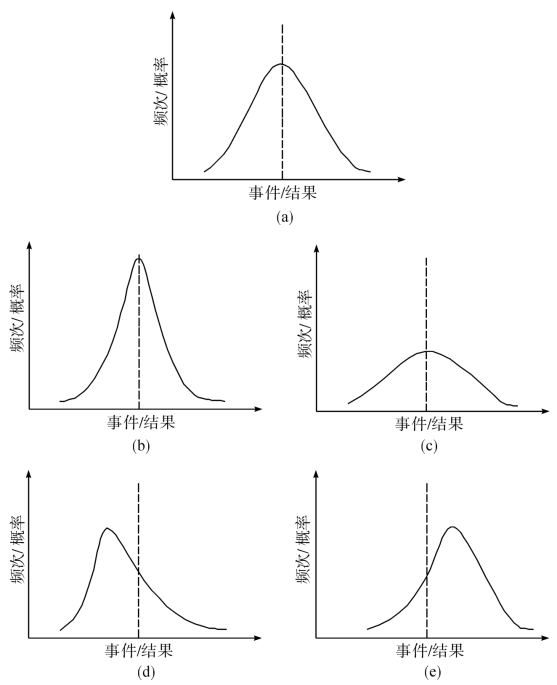
图5-8　危险-风险事件模型各结论分布图

曲线的顶点所对应的横轴坐标,只反映风险评价结果,与辨识的准确性无关。曲线顶点对应的横轴数值偏小的,说明事件发生的整体可能性偏低,结论分散;曲线顶点对应的横轴数值偏大的,说明事件发生的整体可能性很高,结论集中。

任何事物的不确定性或各种可能性,绕不开对熵的讨论。一个危险源可能引发各种连锁事件,最终导致各种事故的发生。在理论模型中,把一个危险源看作附带各种后果的不确定事件集合,因此,可以把“危险源之后”事件的不确定性定义为“风险熵”。广义上讲,风险熵是经验科学对客观世界掌握、改造过程中确定与不确定性的度量,经验科学越具有科学性,风险熵值就越小。风险熵用于分析事件集合变为某些特定事件（或单一事件）的概率。风险熵是对事件集合不确定性的判定数值,可以理解为所有评估人员对企业生产活动进行评估,其评估结果虽然被各种因素影响,但不偏离,并能够真实反映企业的安全生产状况;风险值是对特定事件判定数值,评估人员对类型事件进行模型化分析,其分析结论能较大程度上反映某一点位上的安全生产状况,同时侧面反映评估方法的科学性、可靠性等。风险熵值的意义确定后,对风险值的探讨和使用才具有意义。

概率统计理论中,某个事件实现的概率大,说明其实现的可能性大,事件就越有可能朝着预计的方向发展;反之,某个事件实现的概率小,事件朝着预计方向发展的可能性就小。使用熵值分析,可得到同样的结论:熵值越大,说明事件越混乱,不确定性大,风险大;熵值越小,说明事件越有序,不确定性小,风险小。在这里,不对上述模型进行熵值计算,仅在风险管控评价内容方面进行详细说明。熵在风险评估工作中的意义:宏观上,看似所有的评估工作都是无序杂乱的,评估人员的思维是不统一的,企业环境也是千差万别的,但在科学的评估方法分析下,所有事件的结果均在向某种统一的状态汇集,经过评估人员多次、反复的纠偏更正,事件结果更统一（持续改进,熵值愈小）,而企业在这时就掌握了所有事件大概率（最有可能和最不可能）发生的时序,而我们称之为安全;微观上,评估人员每次的思维活动,抽象事件模型的建立,经验分析等所完成的某方面、专业的评估结论都是有意义的,在日常监测和反馈中不断完善更新,最终接近于真正的科学评价。

结合第一章第三节中对安全与风险的论述,安全从未绝对,风险从未消失。熵值理论下,安全是各种事件集合中,风险熵值最小的那部分集合;风险熵值不可能为零,因此安全不可能本质、绝对。

单个事件都是由多种因素共同影响的结果,多种因素在事件中对结果产生影响的程度也不同。本节主要解决各因素的影响程度和各因素在系统下的结果确定性问题。

以顶板浮石不处理事件为例,顶板浮石的重量、形状、存在高度、人员活动时间、掉落可能性等因素都是变动的,其中,顶板浮石的物理特性在不同企业、不同部门、不同辨识人员的认知中是不同的,这里无法对危险特性进行统一,这是所有风险评估方法的弊端,即不能对特殊性问题进行一般化分析。风险评估方法只能对事件发生的充分必要要素进行统一测量,即暴露（expose）、可能性（possibility）、后果严重性（severity）,对事件起决定性的影响因素。一般因素依据经验分析,决定因素依据分析方法,两种因素累加,确保风险评估结论的准确性、科学性。

综合数据库法已对暴露、可能性和后果严重性三要素的影响程度在分值上已有体现。在横向上,暴露值依据经验总结分为6个数值;在纵向上,暴露、可能性、后果三种因素在分值上为10、10、100。

事件是时序逻辑的因素累加,综合数据库法的风险评估公式:风险值（D）=暴露（E）×可能性（L）×后果（C）,单一因素评价事件的结果呈正态分布,见图5-9。

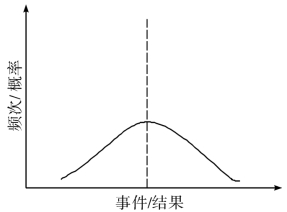
图5-9　单一因素评价事件的正态分布图

当三个因素累积后,其结果呈现“瘦高”形态的正态分布,见图5-10。

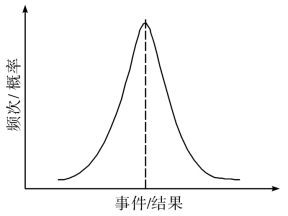
图5-10　多种因素评价事件的正态分布图

把μ值看作是反映实际的、科学的评估结论,三种结果累计后,分布图像比图像更“瘦高”。分布图像中的σ2值偏小,曲线越瘦高,说明是大部分人的共同意见,或某位评估人员大概率的选择结果。在风险评估的实践中表现为:尽管每个人对同一事件的要素基于不同的经验判断,当判别暴露值偏高时,有可能对可能性判别低;当判别后果极其严重的时候,往往对其发生的可能性判别很低;三种因素相累积后,各个因素在计算过程中互相补偿,使得风险值趋于统一稳定。

风险评估人员在无序的评估工作中,基于自身经验分析,运用科学的评估方法,最终结果是各种评估结论大概率地向一个确定的结论靠拢,极小概率地向两边不确定的结论分化,即风险评估结论的“马太效应”。风险评估人员经过多次重复的风险辨识和评估,只能做到辨识评估后的风险结论无限趋近于μ（此处可理解为科学）,却不能等同,正如风险不可能完全清除一样。