基于ICMDS算法的流数据聚类有效性

本书分别基于合成数据集和实测数据集进行验证ICMDS 算法的有效性。

（1）基于合成数据集的ICMDS 算法有效性验证

合成数据集的生成方式与3.5.2 小节的生成方式类似，其生成8 个合成数据集。每个数据集包含100 条流式数据，每条流式数据包含1 000个数据元素。

为了测试ICMDS 随聚类算法的适应性，本实验测试聚类数在2 ～20变化时的聚类性能，所得到的实验结果见表5.5 和表5.6。

表5.5　不同聚类数时4 种算法的聚类准确率

表5.6　不同聚类数时4 种算法的NMI

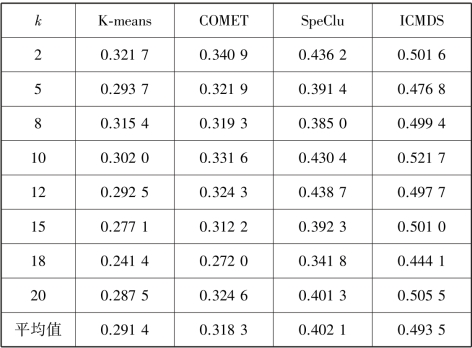
由表5.5 和表5.6 所示的结果可知，ICMDS 和SpeClu 算法比K⁃means和COMET 算法的聚类质量好。其原因在于提出的ICMDS 算法和SpeClu算法考虑了数据的几何结构信息。因为ICMDS 算法考虑了多流式数据之间的相关性随时间不断演化的特性，所以其性能优于SpeClu 算法。

（2）基于实测数据集的ICMDS 算法有效性验证

实测数据集来源于重庆市高速公路24 h×7 d 的道路交通状态记录，本实验选择了北碚隧道、绕城路段、西山坪隧道、渝武路段的从2014 年4月7 日至2014 年5 月4 日共28 天的以5 min 为采样时间所采集交通状态记录。所选路段共包含42 个检测器所采集的交通状态数据。以每一个检测器所采集的交通时间序列为一个流式数据，每条流式数据有8 064个数据记录。

本实验通过表征交通状态的不同参数测试算法ICMDS 的有效性，实验预期为属于同一个方向相近或者相邻检测器所获得的交通状态参数应当表现出耦合关系，同时，由于人类活动的周期变化的相似性。因此，也可能出现空间不相邻相关的某些流式数据之间具有相似性的变化趋势。根据2.3.1 小节的分析，交通参数具有较强的周期特性。本实验以天为单位，所得的ICMDS 与3 种比较算法在7 个时间步上的聚类性能见表5.7和表5.8。(https://www.daowen.com)

表5.7　不同时间步时4 种算法的聚类准确率

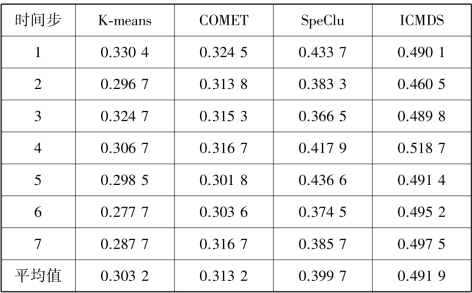
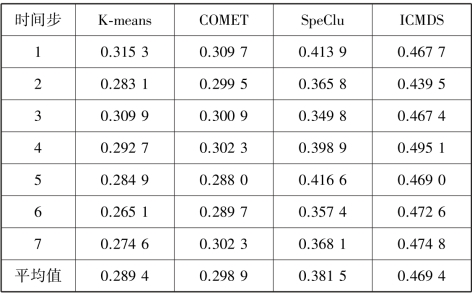
表5.8　不同时间步时4 种算法的NMI

为测试ICMDS 算法在不同聚类数k 时的聚类效果，与3 种相关的比较算法在不同聚类数时的聚类性能见表5.9 和表5.10，包括聚类准确率ACC 和标准互信息NMI。

表5.9　不同聚类数k 时4 种算法的聚类准确率

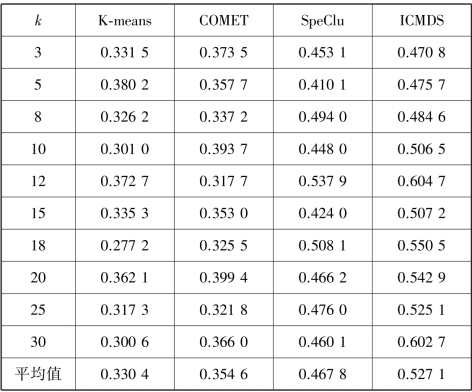
表5.10　不同聚类数k 时4 种算法的NMI

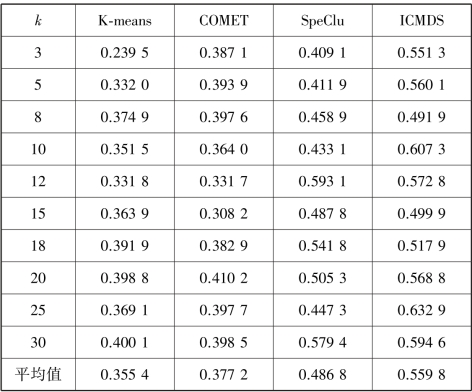
由表5.7—表5.10 所示的结果可知，ICMDS 算法的聚类准确率和NMI 均高于其他3 种算法。其原因在于提出的ICMDS 算法不仅考虑了数据的几何结构信息，还结合了流式数据之间的滞后相关性特点。SpeClu 算法的聚类性能优于COMET 和K⁃means 算法，是因为该算法依赖于数据相似度矩阵的特征结构，当数据空间分布不为凸时，仍然可收敛于全局最优。COMET 和K⁃means 的聚类效果基本一致，本书不作分析。