本节测试提出的EC⁃NMF 方法在实测数据集上的聚类性能。其中，两个数据集分别为Dayton 和PeMS，它们的基本属性见表3.6。

首先，测试EC⁃NMF 应用于Dayton 数据集时的聚类效果。该数据集为世界290 个城市1995 年1 月至2004 年10 月每天的平均气温记录，每个城市代表一个流式数据，每条流式数据有3 416 个数据项。每一年作为一个时间步，一共包括10 个时间序列的数据集。

表3.6　实测数据集的基本属性描述

当α＝0.6 时，EC⁃NMF 在Dayton 数据集上的聚类效果见表3.6 和表3.7，每一个数据集所对应的最好的性能用粗体表示。从表3.7 和表3.8可以看出，EC⁃NMF 算法应用于Dayton 数据集除第一步外大多数时间步上都要优于其他3 种算法，其原因在于EC⁃NMF 算法对流式数据进行聚类时考虑了历史先验信息。

表3.7　当α＝0.6 时，4 种算法在Dayton 数据集上的聚类准确率

续表

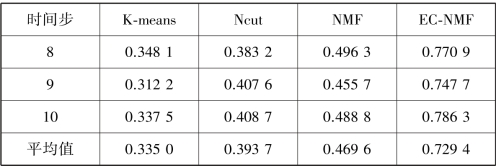
表3.8　当α＝0.6 时，4 种算法在Dayton 数据集上的聚类标准互信息(www.daowen.com)

接下来测试算法EC⁃NMF 应用于PeMS 数据集时的聚类效果。PeMS数据集为实时的交通状态记录。本实验选取了交通状态监控系统中主要记录U.S 高速公路24 h×7 d 的道路交通流量。本实验选择了San Francisco bay 区域从2008 年1 月1 日至2009 年3 月30 日共15 个月每天的交通流量记录。除公共的假期，两天的异常数据以外，以每一天代表一个时间序列的流式数据，该数据集440 个时间序列数据集。本实验的任务是将每一天的数据记录进行分类，如从星期一到星期日，分别标记为ith⁃。

以10 min 为间隔对每一天内的采样数据进行划分，每一条流式数据包括144 个数据项。在一天中一个给定的时间戳内，每一条记录将有963 个（线路，每一条线路为一个站点／检测器）属性。

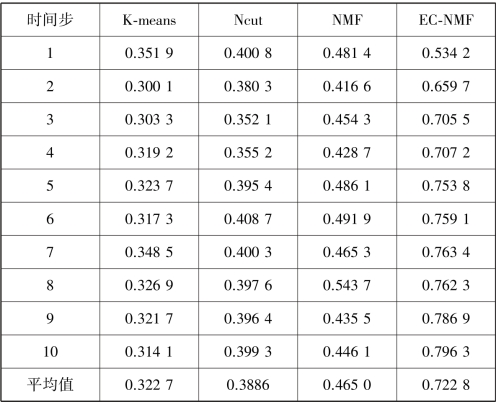
当α＝0.6 时，对于给定的聚类数k，EC⁃NMF 在PeMS 数据集上的聚类效果见表3.9 和表3.10。

表3.9　当α＝0.6 时，4 种算法在PeMS 数据集上的聚类准确率

表3.10　当α＝0.6 时，4 种算法在PeMS 数据集上的聚类标准互信息

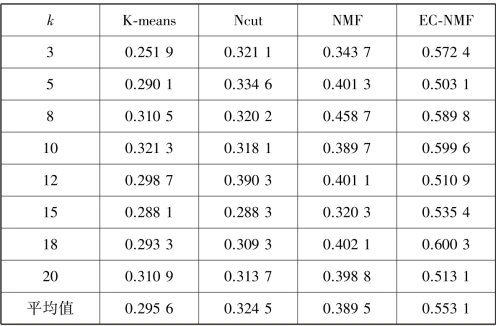
从表3.9 和表3.10 可以看出，Ncut，NMF 以及本书提出的EC⁃NMF 算法的聚类性能均好于传统的K⁃means 算法。其理由是Ncut，NMF 以及本书提出的EC⁃NMF 算法进行聚类时考虑了数据的几何结构信息。EC⁃NMF算法在大多数时间步上都要优于其他3 种算法是因为EC⁃NMF算法不仅考虑了在进行聚类时嵌入了上一步的聚类结果，还利用样本和特征双正则约束的几何结构信息。