为了测试EC⁃NMF 应用于多流式数据时的聚类效果，本书使用原型系统f（·）生成合成数据集［110］。具体的生成方式描述如下： f（t＋Δt）＝f（t）＋f′（t＋Δt），f′（t＋Δt）＝f′（t）＋u（t），t＝0，Δt，2Δt，…。其中，u（t）是分布在区间［－a，a］的独立随机变量。基于原型系统所产生的数据集，分别在水平和垂直方向增加噪声，得到的流式数据S（·）为S（t）＝f（t＋h（t））＋g（t），其中，h（·）和g（·）生成方法与f（·）类似，常量a 决定了过程的流畅度。对于p（·），h（·）和g（·）可以分别设置不同的值，如0.2，0.5，0.6。对于每一个原型函数，通过随机变化在同一个原型系统中生成多条不同的流式数据。

本书随机生成了6 个合成数据集，每个合成数据集的流式数据数目在50～2 000 的合成数据集，每条流式数据包含1 000 个数据元素。每一个方法中，每条流式数据的特征数大小100 个数据点，聚类数为2 ～30。为了得到随机的实验结果，在不同的时间步上对算法进行评价。

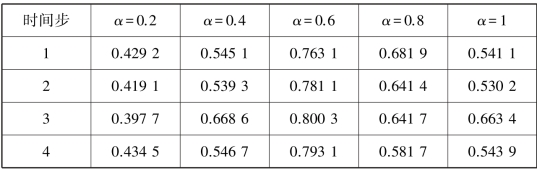
不同的α 大小，代表了历史信息参与的不同程度。当α ＝1 时，没有引入先验信息；当α＝0，仅考虑了先验信息，未对当前时间步的结果进行计算。α 值越大表明了对历史信息的嵌入比例越小。为了测试先验结果对聚类性能的影响，并从中确定出最好的历史信息嵌入比例，本节基于人工合成数据集对α∈［0.2，1］时的聚类性能进行了测试。当α∈［0.2，1］时，不同时间步的EC⁃NMF 的聚类准确率和聚类标准互信息见表3.2 和表3.3。通过表3.2 和表3.3 的结果分析可以发现，当α ＝0.6 时，EC⁃NMF的聚类准确率和聚类标准互信息性能最好。因此，在接下来的实验中，将α＝0.6 作为默认的值对EC⁃NMF 的实际性能进行测试。

表3.2　当α∈［0.2，1］时，算法EC⁃NMF 在合成数据集的聚类准确率

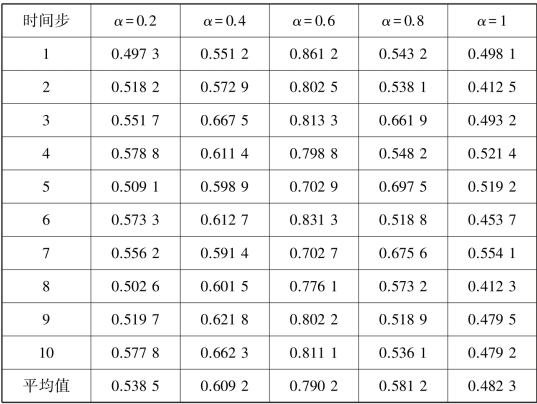
表3.3　当α∈［0.2，1］时，算法EC⁃NMF 在合成数据集的聚类标准互信息

续表

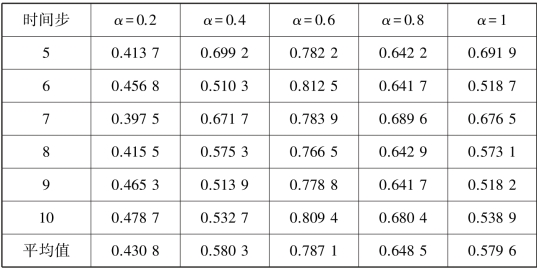
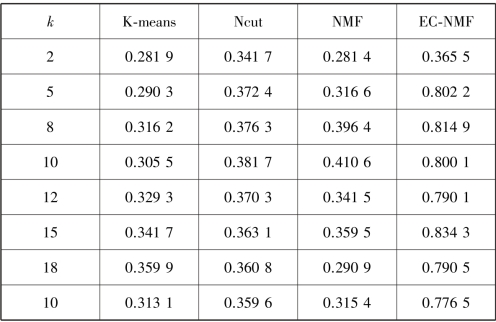
为了测试算法EC⁃NMF 效果，与3 种相关的算法在合成数据集上进行了比较。其中，所有的实验中将α 的值设置为0.6。在不同聚类数的情况下，通过20 次实验所得到的平均聚类准确率和NMI 分别见表3.4 和表3.5。由表3.4 和表3.5 的结果可以看出，考虑了几何结构信息的Ncut，NMF 算法比没有考虑K⁃means 算法的聚类质量好。EC⁃NMF 算法因为考虑了样本属性和特征属性的双正则化约束，所以EC⁃NMF 算法在ACC 和NMI 两个指标上均优于其他3 种算法。

表3.4　4 种算法在合成数据集的聚类准确率

(www.daowen.com)

续表

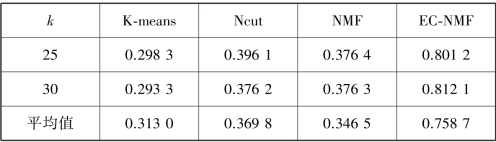
表3.5　4 种算法在合成数据集的聚类标准互信息

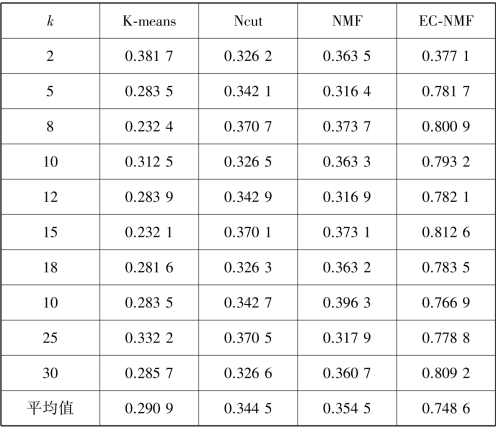
为了测试本章所提出的EC⁃NMF 算法聚类响应时间，接下来的实验中将测试其在不同的聚类数k 和不同的流式数据n 时的时间性能。首先设计聚类数k 从5 变化为300，每一次测试时的流式数据数目为2 000，每一条流式数据包括32 维的特征属性。图3.1 为聚类数k 从5 ～300 变化时的各个算法的聚类响应时间。其中，y⁃axis 代表了执行时间，x⁃axis 代表了聚类数的变化。从图3.1 可以看出，算法EC⁃NMF 和NMF 的执行时间基本一致，且始终优于其他两种算法。

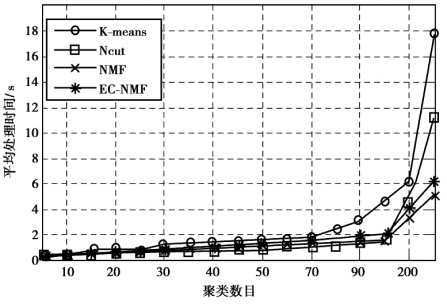
图3.1　当聚类数k 从5～300 变化时，4 种算法的平均处理时间比较

图3.2 为流式数据数量从50 增长为2 000 时的4 种算法的响应时间变化趋势，其中，y⁃axis 代表了执行时间，x⁃axis 代表了流式数据数量的变化，聚类数k＝7。从图3.2 可以看出，除K⁃means 算法以外，流式数据数目从50 变化为2 000 时平均处理时间增长缓慢。其原因在于，Ncut，NMF和EC⁃NMF 算法聚类多流式数据时是在低秩子空间中进行计算，所以3种算法的执行效率高于传统的K⁃means 算法。

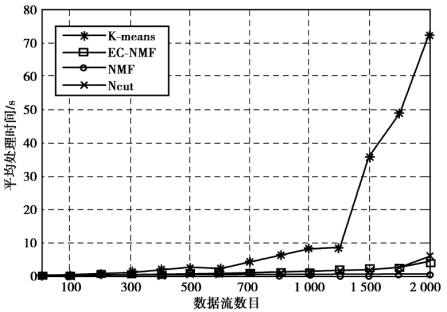
图3.2　当流式数据数n 从50～2 000 时，4 种算法的平均处理时间比较