1．有限元法的基本思路

正如5．1．1节所提到的，在弹塑性力学中，只有少数简单问题能够求得解析解，对于一般的复杂问题，只能通过数值解法进行求解，有限元法是数值解法中十分重要的一种方法，其处理问题的基本思路可以归纳为如下几点：

（1）对连续体进行离散化，即把一个连续体变换成一个离散的结构物，离散结构物是由有限多个、有限大小、形状简单的构件在有限多个点相互联系而组成，如图5－9所示。这些有限大小、形状简单的构件称为有限单元（图5－9中的三角形）。单元与单元之间相互联系的点称为节点（图5－9中的三角形顶点）。并且，连续体的复杂边界也随之变换成由各单元的简单边界所组成。这样一个离散结构物，是真实的连续体的一个近似力学模型，而整个的数值计算就是在这个模型上进行的。

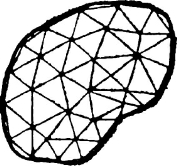
图5－9 连续体的离散化

（2）单元分析，即分析每个单元的力学特性。对于每个单元，根据分块近似的思想，选择一个简单的函数来近似地表示其基本未知量（如位移）的分布规律，并按弹塑性力学的有关理论，建立起各物理量之间的关系式。

（3）整体分析，即对单元分析结果加以综合，以寻求整个离散结构物的分析结果。显然，如果将每个单元比喻为建筑物中的砖瓦，那么将这些砖瓦装配在一起就能提供整个结构的力学特性。

综上所述，用有限元法处理问题的基本思想就是先把连续体分割成有限个简单的单元进行研究，然后再把这些单元的研究结果加以综合，在“一分一合”的过程中，把复杂的连续体计算问题转化为简单构件的分析与综合问题。

为介绍残余应力的数值计算，本小节以涡轮盘热弹塑问题［5］为例进行详细说明，在增量－变刚度法的基础上，应用有限元方法进行求解。

首先，在von Mises屈服准则的基础上推导出弹塑性阶段的应力－应变关系。对于轴对称问题，设全应力列阵为

全应变列阵为

在弹性范围内有

其中，D为弹性矩阵。

在讨论塑性问题时，将σ，ε分解为两部分，如下式所列：

式中，σH和εH为静水分量，即

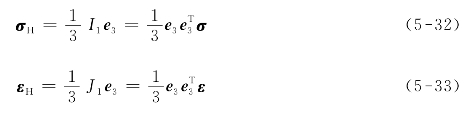
式中，e3＝［1 1 1 0］T，I1＝σR＋σθ＋σZ，J1＝εR＋εθ＋εZ。

将式（5－32）与式（5－33）代入式（5－30）与式（5－31）中，可得到应力偏量与应变偏量：

式中，，而I4为4×4的单位阵。

在塑性理论中，von Mises屈服准则是

式中，是等效应力，它等于简单轴向拉伸的屈服应力，当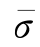达到屈服极限时，塑性变形就开始发生。

而等效塑性应变是

式中，εp为塑性应变。

根据塑性理论的流动定律，塑性应变可写成

式中，λ为比例常数。将式（5－36）代入式（5－38），得

由式（5－37）有

以式（5－39）代入，并利用式（5－36），可得

由此得

利用式（5－42），将式（5－39）改写为

利用简单轴向拉伸试验得到的应力－塑性应变关系，可得斜率公式

式中，下标u表示单轴拉伸。

将式（5－44）代入式（5－43），可得

将式（5－36）写成增量形式：

(www.daowen.com)

即

由式（5－45），得

记s＝则有

式（5－49）就是弹塑性阶段内应力－塑性应变的增量关系。

若以Δεe表示弹性应变的增量，则有

全应变增量为弹性应变增量与塑性应变增量的组合，即

对式（5－51）求逆，可得

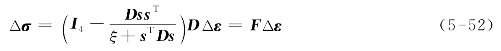
式中，F可视为材料的弹塑性矩阵，在弹塑性阶段F取代了D，显然，对于理想塑性材料，取ξ＝0。

从屈服准则式（5－36）中可导出轴对称问题的等效应力公式：

由于弹塑性阶段无法像弹性情况那样建立最终应力状态和最终应变状态的全量关系，而只能建立反映依赖加载路径和加载方式的应力－应变之间的增量关系，也就是说结构开始进入屈服时，载荷增量是按小的增量步一步一步往上加，例如设R为结构开始进入塑性时对应的载荷，增量步可取为0．05R～0．1R，每增加一次载荷就会引起位移、应变及应力的相应变化。分别记位移、应变及应力增量为Δδ，Δε，Δσ，只要增加的载荷适当小，则应力增量和应变增量之间的关系可表示为

式中，F不包含有应力和应变的增量，而仅与加载前的应力水平有关，即成了一个线性式子。

增量形式的平衡方程为

式中，ΔR是载荷增量。对每次加载刚度矩阵都发生变化，该方法就称为增量——变刚度法。

接着，需要构建结构的刚度矩阵，对于弹性状态的单元而言，其刚度矩阵为

对于塑性状态的单元，其刚度矩阵为

对于与塑性单元邻近，在增量加载前处于弹性状态，但在加载后将进入屈服的“过渡区域”中的单元，采用加权平均的方法，即取它们的刚度矩阵为

式中，＝mD＋（1－m）F，为加权平均弹塑性矩阵，而加权因子为

式中 σs——屈服极限；

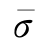——加载前达到的等效应力水平；

Δ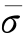——加载后估计可能得到的等效应力增量。

对Δ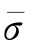的估计，一次不能精确，需要一个迭代的过程。一般，第一次估计时，把过渡区域的单元作弹性处理，再利用计算结果修正Δ和m，通常2～3次迭代后就能得到较为精确的m值。

航空发动机的工作处于地—空—地的循环之中，若结构进入塑性，则卸载后结构内将产生残余变形及残余应力。设卸载前的位移、应力分别为δp和σp，它们是加载过程计算得到的，在此基础上卸载就可以求出残余应变和残余应力，由于卸载时，结构呈弹性特性，故一般可一次求解

式中，R是加载过程中所施加的全部载荷。从式（5－60）求得卸载产生的位移δe、应变εe和应力σe后，残余位移、残余应变和残余应力为

2．有限元求解的具体步骤

归纳起来，整个有限元求解过程可分为以下几个步骤：

（1）对结构施加全部载荷R，作纯弹性计算。

（2）求出各单元的等效应力，并记其最大值为，令再用WR作弹性计算，所得应变、应力等均为初始屈服时的值，然后以作为每一步加载的载荷增量，进行逐步加载，n为加载步数。

（3）施加载荷增量ΔR，先置m＝0，解KΔδ＝ΔR，估计各单元可能引起的等效应力增量Δ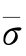，并由式（5－59）求解m值。

（4）对每一个单元按落在弹性区、塑性区或过渡区域的不同情况，分别形成单元刚度矩阵。

（5）叠加元素刚度矩阵为总刚度矩阵，并求出位移增量、应变增量及等效应力增量，据此修改Δ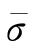和m。

（6）重复步骤（4）和（5）2～3次。

（7）计算位移和应力增量，并把它们叠加到这一步加载前的水平上去。

（8）重复步骤（3）—（7），直到载荷全部加完为止。

（9）作卸载计算，求出最终的残余位移、残余应变以及残余应力。