往往工厂与工地现场缺乏测量设备而又急需掌握残余应力数量级概念，以便及时对现场故障进行分析处理，为此，有人提出一种估算残余应力的经验公式：

式中 k——常系数；

p——相变系数，它与工件的冷却速度、淬火热处理或焊接时的加热温度、回火温度、碳钢中的含碳量及合金钢中所含的合金元素与品种等诸多因素有关；

q——几何系数，它与工件的形状、尺寸等因素有关；

t——工艺系数，它随渗碳、渗氮、冷拔、磨削、滚轧等不同的工艺有关。

残余应力估算公式虽具有较为简洁的一般形式，但所涉及的系数众多，且较难确定合适的数值大小，因此该种估算方法十分粗糙。如今残余应力工程估算的发展思路是，在一定的理论基础之上，结合相关试验结果并拟合试验数据，得到一个针对某一具体问题的经验公式，并在此基础上做适当推广。该种方法能够大幅提升残余应力估算的精度，下面以激光冲击波诱发的钢材料残余应力的估算［2］进行简单说明。

1．激光冲击的基本力学模型

研究激光冲击力学模型时，做如下假设：假设被冲击工件材料为理想的钢塑性材料，在强冲击载荷的作用下，通常要发生大的塑性形变，冲击能量所做的功绝大部分要转变为塑性形变，只有小部分消耗于弹性能。所以，不仅可以忽略材料的弹性形变，而且可以忽略材料的应变强化效应。激光冲击力学效应的物理模型如图5－5所示。

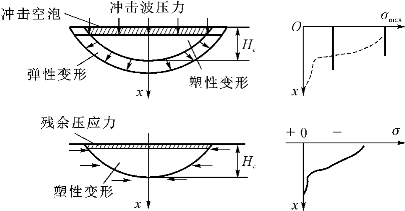
图5－5 激光冲击塑性形变与力学效应示意图

图5－6 冲击形变微元体示意图

激光冲击应力波为一维平面波，在激光冲击区取一个微体积元（图5－6），仅在z方向考虑被压缩，即冲击波沿z方向传播。考虑应力和应变的关系，为保持σx的单轴应变条件而假设σy＝σz，仅x方向有弹塑性形变。激光冲击后弹性形变恢复不完全，导致了残余应力的产生。激光产生的冲击波压力在x方向上衰减很快，衰减程度取决于材料密度和材料本身的力学性能。定义冲击强化层厚度Hc为在x方向的金属工件表面至塑性形变边界区的距离，对应在宏观效应上，冲击区的硬度随着x的增大而下降，且残余应力与硬度增量有着对应关系。

2．残余应力计算公式的力学模型

根据Mises屈服准则有

在弹性范围内，应力与应变关系为

式中，θ＝εx＋εy＋εz，因为是单轴形变，侧面受到介质约束εx＝（V0－V）／V，εy＝εz＝0，V为体积，V0为形变后体积，λ和μ为材料的拉梅常数，ν为泊松比，ν＝λ／［2（λ＋μ）］。

在塑性形变状态下，应变增量是弹性增量和塑性增量之和。因而在x方向有：

因为不存在塑性膨胀，所以

(www.daowen.com)

微元体中的残余应力是由弹性和塑性形变引起的：

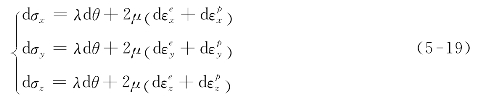
激光冲击应力作用后，在冲击强化区的y，z方向上由弹性应力引起的弹性形变难以完全恢复，所以，在激光冲击区形成残余应力，于是可得简单计算式：

实际上，σx是随着冲击应力波的衰减而变化，故残余应力σy也是随着x的变化而变化，设［3］

有

式中，b为参量，另外根据激光冲击波峰压公式：

式中 ρ——等离子体密度；

A——涂层吸收率；

q0——激光功率密度。

若将σmax＝Pmax代入式（5－22）和式（5－23）中，则可得到Pmax未卸载时的残余应力，但此时的表达式用于估算残余应力是十分粗糙的，此处利用文献［4］中的数据进行对比，通过公式得到的残余应力值为－1．14GPa，而实测值却只有－400MPa，因此对于估算公式的修正将是残余应力估算极其重要的一环。

由弹性力学原理可知，当材料受到相同外力作用时，弹性模量越大，弹塑性变形就越小。因此，当x方向受到一定的冲击波压力时，如果材料的弹性模量E大，则形变体周边材料越接近于刚体，那么形变体y，z方向上产生的残余应力相应就越大，因此有σx∝E。同时，结合冲击动力学原理，当材料的冲击形变深度相同时，材料本身的弹性模量大，屈服极限高，冲击波对材料产生残余应力的影响大，即残余应力的衰减慢，因此有σx∝e－bx／E。最终得到修正后的公式如下：

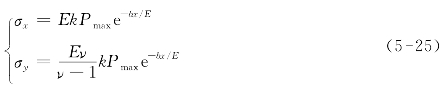
根据相关试验数据，采用最小二乘法可拟合求得k，b的值，此时该激光冲击残余应力估算公式具有一般适用性。

3．实验验证

激光冲击强化实验所用材料为40Cr和45＃钢，弹性模量分别为211GPa和201GPa，泊松比分别为0．277和0．293。实验所用激光冲击参数：光斑直径均为7mm，脉冲时间均为23ns，涂层吸收率A均为0．8，等离子体密度ρ均为1 500kg／m3，激光功率密度q0分别为2．35GW／cm2和2．03GW／cm2。根据式（5－24），可计算得到它们的冲击峰值压力分别为2．3GPa和2．1GPa。40Cr和45＃钢利用估算公式所得的残余应力计算值与实测值对比图如图5－7、图5－8所示。由图中可以看出，修正后的估算公式准确性较高，适用性较好。

图5－7 40Cr钢的残余应力计算值和实测值的对比图

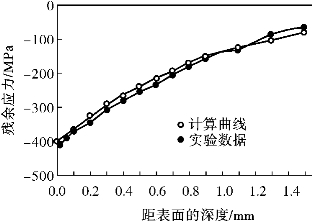
图5－8 45＃钢的残余应力计算值和实测值的对比图