当构件处于弹塑性状态时，若将外载荷卸除，则不但留有残余变形，而且留有残余应力。当材料超过屈服极限后，其应力－应变关系在加载时按塑性规律变化，而在卸载时按弹性规律变化，在一定条件下，由于二者应力分布规律的差异而引起了残余应力。

设加载应力为σ，卸载应力为σ′，则残余应力为

通过两个实例进行简单说明。

1．纯弯曲矩形界面简支梁的残余应力

（1）理想弹塑性材料梁。设矩形截面梁宽为b，高为h，则对应于图5－1（a），（c），弹性极限弯矩及塑性极限弯矩分别为

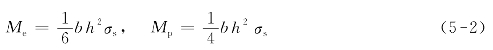
图5－1（b）所对应的“部分塑性”截面弯矩为

式中，ξ是弹性区尺寸，超过则构件进入塑性区。

由式（5－3）知，当ξ＝h时，即为图5－1（a）所示情形；当ξ＝0时，即为图5－1（c）所示情形。

设在图5－1（b）所示情形开始卸载，则按弹性规律变化的卸载应力为

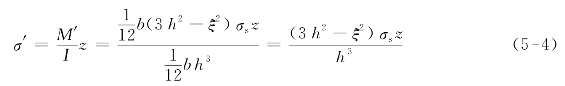
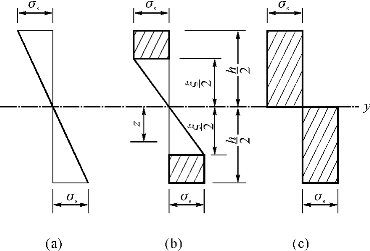
图5－1 截面应力变化

截面残余应力分布如图5－2所示，残余应力对应的计算公式为

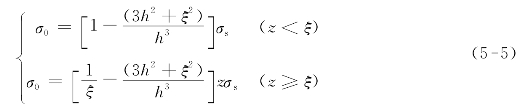
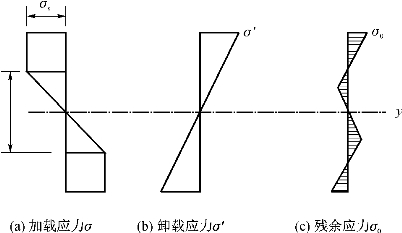
图5－2 理想弹塑性材料梁

（2）线性硬化材料梁。设矩形截面梁高为h，宽为b，则“部分塑性”截面弯矩为

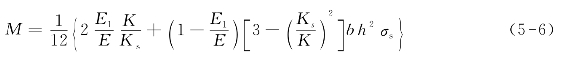(www.daowen.com)

式中，E1见图5－3（a），Ks＝2σs／（Eh）；根据式（5－6）可绘制M－K曲率图，于是可由M确定K，而由式εmax＝bk／2确定εmax，再由单向拉伸图5－3（a）确定对应的σmax，而

由式（5－7）可求得h，从而可确定截面应力分布图［图5－3（c）］。

同样，卸载应力按弹性规律，如图5－3（b）所示。设式（5－6）加载到M，然后卸载，则卸载应力为

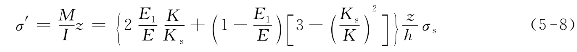
如图5－3（e）所示，残余应力为

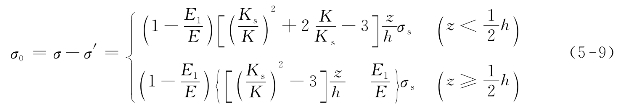
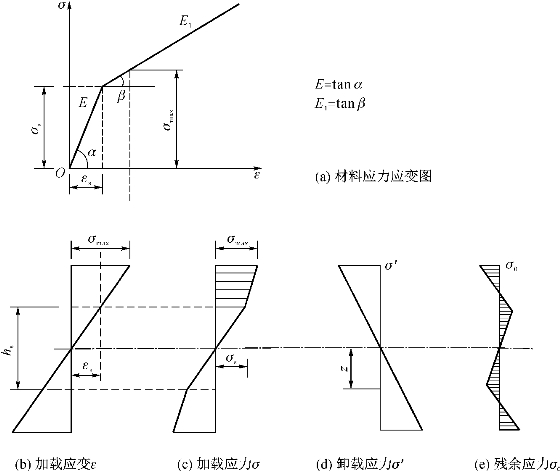
图5－3 线性硬化材料梁

2．理想弹塑性材料圆周扭转的残余应力

内半径为a，外半径为b的空心圆截面柱体，并令c＝a／b，则加载时弹性极限扭矩［图5－4（a）］为

式中，τs为剪切屈服应力。而塑性极限扭矩［图5－4（b）］为

设当截面全部屈服［图5－4（b）］后卸载，则卸载应力［图5－4（c）］为

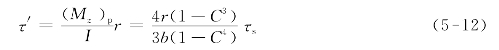
则残余应力［图5－4（d）］为

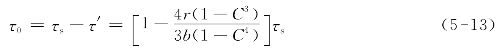
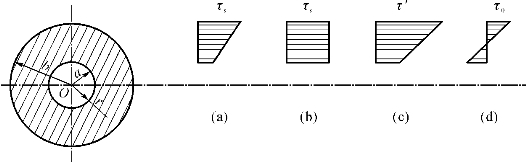
图5－4 空心圆轴在加载与卸载情况下的应力分布