材料体积单元中存在6个应力分量，σx，σy，σz分别为x轴、y轴、z轴方向的正应力分量，τx，τy，τz分别表示三个方向切应力分量。图4－7为直角坐标系，其中σ1、σ2分别表示平面内应力的最大值和最小值，φ和ψ为空间任意方向OP的两个方位角，ψ为OP与样品表面法线的夹角，φ是OP在样品平面上的投影与x轴的夹角，εφψ为材料沿OP方向的弹性应变，如图4－7所示。

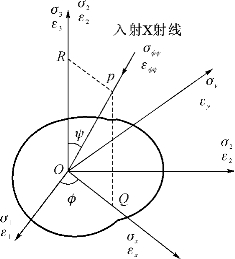
图4－7 应力测量空间坐标

根据弹性力学理论，应变εφψ可表示为

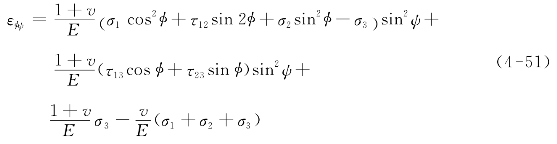
式中 E——材料的弹性模量；

ν——泊松比。

此公式为宏观应力和应变之间的关系。根据布拉格方程，此处应变：

式中，d0是材料无应力状态的晶面间距，此公式为晶面间距和应变的关系。将式（4－51）与式（4－52）相结合则可以通过微观的晶面间距求得宏观应力，此为X射线检测残余应力的理论基础。X射线的穿透能力较弱，只能测得材料表面的残余应力，可以将材料表面的应力视为二维应力，法线方向应力为零，即σz＝τxz＝τyz＝0。将方位角φ分别设为0°，90°和45°，并对式（4－51）中的sin2ψ求偏导，整理，得：

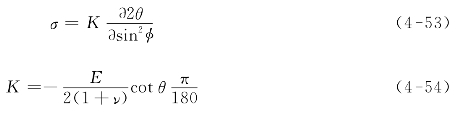
式（4－54）中的K被定义为X射线应力常数，为试验测得，本公式为X射线衍射法检测残余应力的基本公式。

1．传统sin2ψ法

假设选择n个ψ角进行测量，那么最小二乘法的结果为

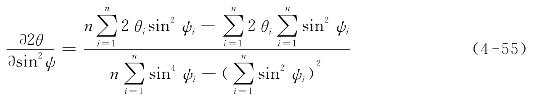(www.daowen.com)

最后利用公式，用已知的应力常数与斜率相乘就可获得最终的残余应力数值。根据ψ平面和2θ所在平面的关系，应力测量方法可以分为同倾法和侧倾法两种测量方式。同倾法的衍射几何特点是ψ平面与测角仪2θ扫描平面重合。而同倾法又分为固定ψ0法和固定ψ法。固定ψ0法在反射X射线的接收过程中入射角ψ0保持不变，在应力测试过程中，通过改变入射线与试样表面法线之间的夹角ψ0来计算残余应力；固定ψ法的原理是在测角头扫描的过程中，2θ角的衍射面的法线固定在不变的ψ角方向。在测量过程中，X射线管与探测器等速相向（或相反）而行，固定晶面法线的入射角与反射角相等时接收反射X射线，通过改变一系列衍射晶面法线与试样表面法线的夹角ψ来检测残余应力。这两种同倾法都适用于应力仪检测残余应力。

2．cosα法

近年来，二维探测器处于快速发展阶段，这种探测器可以收集衍射环的衍射信息，已经集成在同步辐射仪器或者实验室的测试系统中，并已应用于不同材料的应力分析中。当用二维探测器进行应力测量时，在每个样品方向上，衍射环的畸变可直接用于应力计算。此外，结合二维图像的强度，可以获得2θ角平面的图形，并利用传统的粉末衍射分析软件对其进行分析。二维探测器与微束衍射相结合，使得X射线衍射技术在尺寸缩小的器件、元件、薄膜和涂层上有了新的应用。应力实测的角度设置如图4－7所示。当试件在平面应力作用下，沿德拜环圆周角α方向的法向应变为

常数项a0不影响测试结果，因此被省略。这里将上式看作近似平面应力。可以用与应力测试有关的杨氏模量E和泊松比ν来表示上述公式的各项系数。

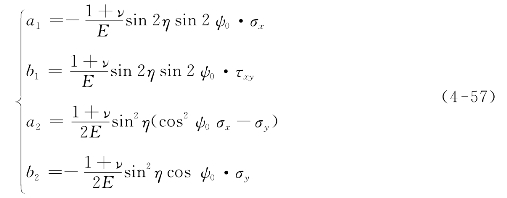
式（4－57）中，η是衍射角θ的互余角，ψ0是样品表面法线与X射线入射角之间的夹角，而σx，σy和τxy分别是纵向应力、横向应力和剪切应力。值得注意的是，ψ0与传统上表示试样表面相对于衍射矢量的法向倾角的ψ不同。为了简化，在下面的讨论中，将ψ0称为“X射线入射角”或“入射角”。试件的应力可用下列公式来计算。

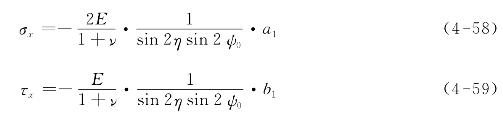
德拜环在前衍射角（2θ＜90°）给出了更多关于应力张量评估的信息，由于ψ角的虚拟扫描覆盖范围很大（从0°到大约80°，这取决于2θ的位置和图像板的大小）。在薄膜或者涂层材料中，经常在只有在小角度下才有明确的峰值，可以利用此方法计算残余应力［8］。通过上述讨论，发现通过单次曝光，用一个X射线衍射图像就可以计算选定方向的残余应力。这种测试方法的优点是：

（1）单次曝光，测量时间更短；

（2）固定的样品位置和光束位置，因此不存在机械衍射元件旋转带来的统计误差；

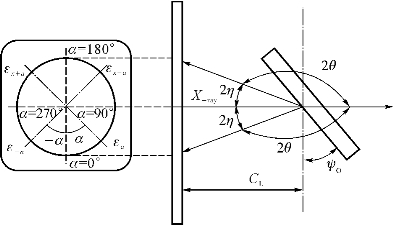
图4－8 应力测量角度

（3）由于入射角固定，所以测试深度固定。