1．方法A：高速钻孔残余应力的计算方法

1）薄工件均匀应力计算

（1）根据测得的释放应变ε1，ε2和ε3，按式（4－3）、式（4－4）和式（4－5）计算下面的组合应变：

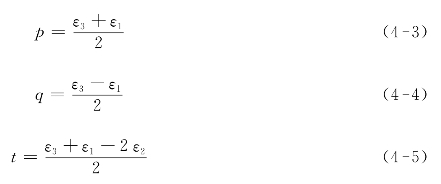
（2）根据GB／T 31310—2014的规定，通过孔径大小和应变花类型来选择标定常数a和b。

（3）将组合应变p，q和t代入式（4－6）、式（4－7）和式（4－8）分别计算三个组合应力P，Q和T：

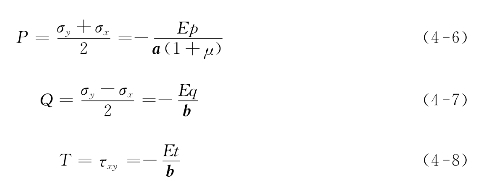
（4）按式（4－9）、式（4－10）和式（4－11）分别计算平面笛卡儿坐标系下应力值σx，σy和τxy：

（5）按式（4－12）计算主应力σmax和σmin：

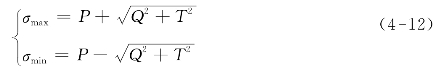
如图4－2所示，最大拉伸（或最小压缩）主应力σmax位于从1＃敏感栅方向起顺时针转过β角的方向。与此类似，最小拉伸（或最大压缩）σmin主应力位于从3＃敏感栅方向起顺时针转过β角的方向。

（6）按式（4－13）计算β角：

可利用单一自变量反正切函数来计算β角，一般的计算器都具备该功能，但是它可能会与真值间相差±90°。正确的角度值可以通过双自变量反正切函数来计算（在有些计算机命令中为atan2），该函数中分子和分母的符号是分开考虑的。或者，将单一自变量反正切函数的计算结果通过增加或减去90°，使其达到表4－2所规定的角度范围。

表4－2 主应力方向角β

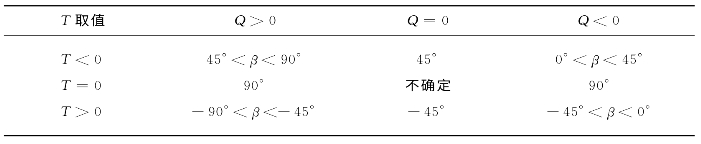
（7）β角为正值，如β＝30°，表示σmax在1＃敏感栅顺时针转动30°的方向上。β角为负值，如β＝－30°，表示σmax在1＃敏感栅逆时针转动30°的方向上。一般来讲，σmax的方向与绝对值最大且符号为负（压缩）应变的方向相一致。

注：β角的转动方向仅是针对敏感栅采用顺时针编号规则的应变花，例如图4－2所示的应变花。如果敏感栅编号采用的是逆时针编号规则，那么β角就应逆时针旋转。后者的1＃和3＃敏感栅的位置相对于前者刚好互换，新定义的1＃敏感栅方向成了参考方向。当使用逆时针编号敏感栅时，如果β角为正值，如β＝30°表示σmax在1＃敏感栅逆时针转动30°的方向上。除此之外，顺时针编号敏感栅和逆时针编号敏感栅在计算方法上都是相同的。

（8）如果计算所得的主应力超过了材料屈服强度的60%，即表明孔边材料发生了局部屈服。这种情况下无法给出定量的结果，只能给出“定性”的报告。总体上，当计算得到的应力值超过材料屈服强度的60%时，即提示该应力值有所高估，实际值应比计算结果偏小一些。

2）厚工件均匀应力计算

（1）绘制应变ε1，ε2和ε3与孔深间的关系曲线，确认数据点的变化趋势较为平滑。对存在较大误差和明显偏离主曲线的数据点应进行筛查，必要时重新钻孔。

（2）根据不同深度下测得的ε1，ε2和ε3，采用式（4－3）—式（4－5）计算与之相关的组合应变p，q和t 。

（3）为了验证残余应力沿孔深方向上是否大小一致，首先需要从各个孔深中挑选出q或t绝对值较大的那一组数据，将该处测得的组合应变p以及较大的q和t分别除以最大孔深所对应的组合应变（用百分比表示）。绘制这些百分比与对应孔深间的关系曲线。所得到的图形应与图4－6中的曲线很相近［11］。如果所得数据点明显偏离图4－6中的曲线（超过±3%），则表明应力分布沿厚度方向是不均匀的，或者是应变测量存在较大误差。无论是哪种情况，这些数据都无法用于均匀应力场的计算，而采用非均匀应力测量方式会更合适一些。

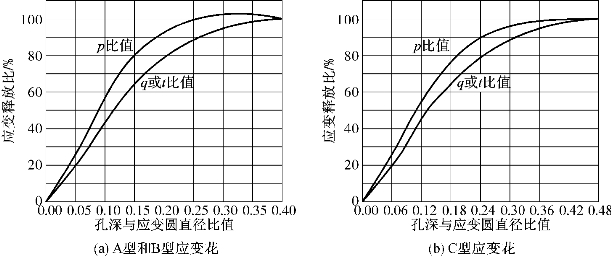
图4－6 应变释放比与孔深关系曲线（应力沿厚度方向均匀分布）

注：上述图形化的验证方式对均匀应力场并非足够敏感，那些具有非均匀应力场的工件也会呈现类似图4－6的应变曲线。该验证实验的主要目的是大致筛查出非均匀应力场以及应变测屈误差，该验证实验仅对“厚”工件适用。

（4）在8个不同孔深处测得应变值ε1，ε2和ε3，根据表4－2选择不同孔深，孔径及应变花所对应的标定常数a和b。表中的数据根据有限元分析得到。

（5）由相应的组合应变p和q和t按式（4－14）、式（4－15）和式（4－16）分别计算三个组合应力P，Q和T，其中，∑表示指定变屈在8个孔深处的总和。

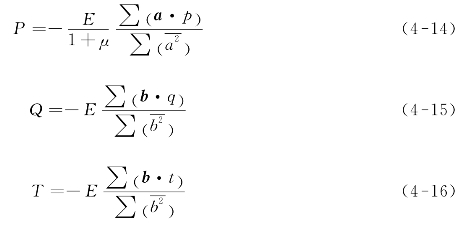
注：可以仅将一组数据ε1，ε2和ε3，例如最大孔深处的应变测量值代入式（4－3）—式（4－8）计算出组合应力P，Q和T，采用该方式可对残余应力进行快速评估。然而应优先采用此处的平均计算方式，因为该方式将所有数据点都纳入计算，可以显著降低随机误差［12］。

（6）根据薄工件中的步骤（5）～（8）计算笛卡儿应力σx，σy和τxy，主应力σmax和σmin以及主应力方向角β。

3）中等厚度工件均匀应力计算

对于那些介于薄工件和厚工件之间的中等厚度工件不在本标准的技术范围内。如果工件的应力分布较为均匀，可以用表4－2中给出的“通孔”以及“盲孔”和“通”孔标定数据的内插值得到近似结果，采用这种方式计算出的残余应力应注明为“非标准”和“近似”结果。

2．非均匀应力计算

1）应变数据

（1）绘制应变ε1，ε2和ε3与孔深间的关系曲线，确认数据点的变化趋势较为平滑。对存在较大误差和明显偏离主曲线的数据点应进行筛查，必要时重新钻孔。

（2）根据不同深度下测得的ε1，ε2和ε3，代入式（4－17）—式（4－19）分别计算组合应变。

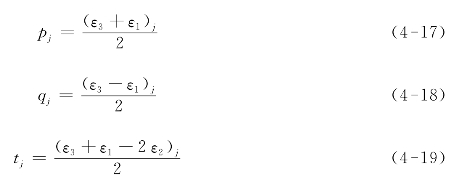
注：式中的下标j代表应变值ε1，ε2和ε3所对应的不同步进深度序号。

（3）按式（4－20）—式（4－22）分别估算组合应变的标准差［13］：

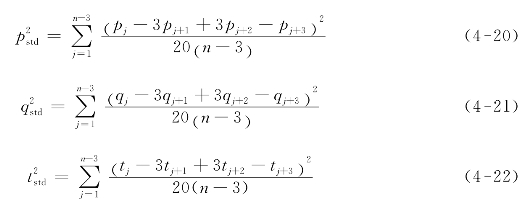
注：式中的n代表不同步进深度下所测应变值的序号，求和的取值范围1≤j≤n－3。

2）标定矩阵

（1）如果选择A型应变花，则采用《金属材料 残余应力测定 钻孔应变法》（GB／T 31310—2014）中表6和表7中的标定数据组成矩阵ajk和bjk。该表所列常数对应的是目前应用最为普遍的公称尺寸为1／16英寸的应变花。如果采用1／32英寸的应变花，则需将所有孔深和步进深度数据乘以修正系数0．5。如果采用1／8英寸的应变花，则需乘以修正系数2。

（2）如果选择B型应变花，则采用《金属材料 残余应力测定 钻孔应变法》（GB／T 31310—2014）中表8和表9中的标定数据组成矩阵ajk和bjk，如果选择C型应变花，则需采用标准中表10和表11中的数据。B型和C型应变花通常仅有1／16英寸的一个公称尺寸。

（3）《金属材料 残余应力测定 钻孔应变法》（GB／T 31310—2014）中表6和表11中数值所对应的孔径均为2mm，如果孔径实际测量值D0与其不一致，则需乘以修正系数（D0／2mm）2。

注1：采用国际单位mm与英制单位inch所计算的结果差异较小，可以忽略该影响。

注2：《金属材料 残余应力测定 钻孔应变法》（GB／T 31310—2014）中表6和表11中所列数值均保留到小数点后5位数字，这是为了在进行矩阵计算时减少修约误差，实际上个别数据没有这么高的精度。

3）应力计算方法

（1）采用积分方式可以计算出不同孔深所对应的残余应力，其应变值需要求解下列矩阵方程：

以上公式中：(www.daowen.com)

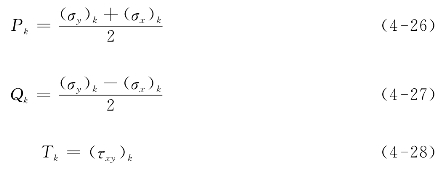
组合应变p，q和t可根据式（4－17）—式（4－19）确定。当钻孔所采用的步进次数较小时，可采用式（4－23）—式（4－25）计算残余应力。然而当钻孔所采用的步进次数较多时，矩阵a和矩阵b成了病态矩阵，在这种情况下，少许的应变测量误差可能导致应力计算结果产生很大的误差。为了减少这种效应，可采用下述的Tikhonov正则化方法。

（2）组成三对角“二阶导数”矩阵c：

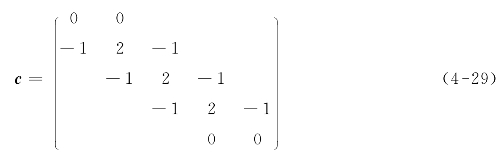
矩阵的行等于钻孔所采用的步进次数，第一行和最后一行为零，其余各行数据［－1 2 －1］沿对角线对称分布。

（3）使用矩阵c代入式（4－23）—式（4－25）来实现Tikhonov二阶导数（平滑模型）正则化：

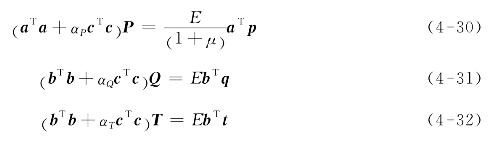
（4）应力调整因子αP，αQ和αT预设值的大小会影响到运算的次数，采用该方法进行运算会使应力结果更加平滑。如果因子为零，则式（4－30）—式（4－32）与先前未采用该方法的式（4－23）—式（4－25）是等同的。当选择较大的符号为正的调整因子时，曲线的平滑效果明显。如果调整因子过小的话，会在曲线上留有异常噪声，这种异常噪声会导致结果失真，在选择最优的调整参数时需处理好二者之间的关系。

（5）首先预设较小的调整因子αP，αQ和αT，取值范围在10－6～10－4之间为宜，求解式（4－30）—式（4－32）获得应力P，Q和T。

（6）由于采用了Tikhonov（平滑模型）正则化方法，未经平滑处理的应变数据代入式（4－23）—式（4－25）所计算出的组合应力P，Q和T与平滑后的应变数据p，q和t无法准确对应，二者间的差异采用失配向量（misfit）表示，见式（4－33）—式（4－35）。

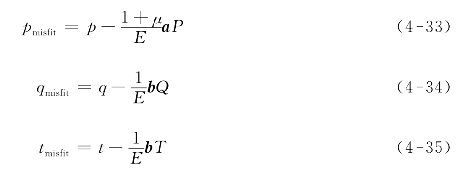
（7）计算“misfit”失配向量均值的平方，见式（4－36）—式（4－38）。

（8）如果与式（4－20）—式（4－22）中的之间的差异小于5%，可以认为组合应力P，Q和T的计算结果可信，否则需要重新估计新的调整因子。

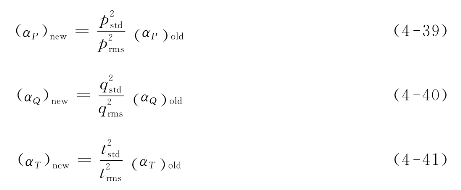
（9）根据式（4－30）—式（4－41）重新计算新的组合应力P，Q和T，直到满足差异小于5%的判据。

（10）按式（4－42）、式（4－43）和式（4－44）分别计算：

（11）按式（4－45）和按式（4－46）计算主应力和方向角：

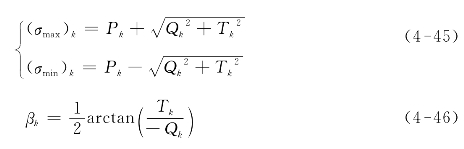
（12）以采用双自变量反正切函数（在有些计算机命令中为atan2）来确定P的象限角，或者将单自变量反正切函数的计算结果增加或减去90°，使其大小刚好处在表4－3所示的角度范围内。

（13）如果P角为正值，例如β＝30°，表示σmax位于1＃应变计顺时针转动30°的方向上；如果β角为负值，如β＝－30°表示σmax位于1＃应变计逆时针转动30°的方向上。

（14）通常，σmax的方向与数值上绝对值最大且符号为负的（压缩）应变的方向紧密相关。当组合应力Q和T同时为零时，则表示该处为各向同性应力场，β角无意义。

（15）绘制σmax和σmin与孔深的关系曲线，如果计算所得的应力超过了材料屈服强度值的60%，这种情况下无法给出定量的结果，只能给出“定性”的报告。当计算得到的应力超过材料屈服强度值的60%时，即提示该应力值有所高估，真实值通常比计算结果偏小。

3．残余应力测量原始记录

1）均匀应力薄工件

（1）每个应变花上的应变读数。

（2）计算每个应变花上的x方向、y方向应力以及主应力。

2）均匀应力厚工件

（1）绘制每个应变花所对应的应变－孔深关系曲线。

（2）将每个应变花上的应变ε1，ε2和ε3列表。

（3）计算每个应变花上的x方向、y方向应力以及主应力。

3）非均匀应力状态厚工件

（1）绘制每个应变花所对应的应变－孔深关系曲线。

（2）将每个应变花上的ε1，ε2和ε3列表。

（3）估计每个应变花上的应变标准差。

（4）绘制每个应变花所对应的x方向、y方向应力－孔深关系曲线并列表。

（5）将每个应变花上的主应力和主方向角列表。

4．方法B：低速钻孔残余应力计算方法

（1）采用低速钻技术（一般为手电钻），钻孔时的加工应变特别明显。另外考虑到该方法经常用在高残余应力场合，所以应力标定常数的确定应采用4．3节中的试验标定方法获取。

（2）由于手工钻孔时的下压速度很难控制，所以钻孔时不再分步，而是一次钻到规定深度1．2 D0。

（3）根据测得的应变ε1，ε2和ε3和按式（4－3）—式（4－5）计算组合应变。

（4）根据式（4－47）计算主应力σmax和σmin：

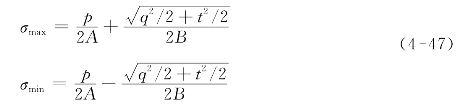
式中，A，B为应力标定常数。

初次计算时采用0．3σs对应的系数，如果所得应力接近材料的0．7σs或0．9σs，再选用相应应力下的A，B标定系数重新计算。

（5）方向角按照薄工件计算方法计算。

（6）如果计算沿应变计1和3方向的应力值，则按式（4－48）—式（4－49）计算：

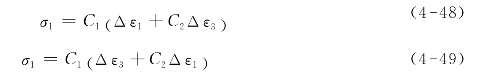
式中，C1＝（A＋B）／（4AB）；C2＝（B－A）／（A＋B）。