1．工件

（1）工件上的测点应选择在一个平坦的表面，同时应注意避免在工件边缘或其他不规则部位。图4－1显示了钻孔后测点部位的应力分布情况。假设这些应力在x－y平面内是均匀分布的。

（2）如图4－1（a）所示，工件内的残余应力沿孔深方向大小是一致的。在x－y平面内的应力有σx，σy和τxy。可采用这种方式测量薄工件内的均匀残余应力，对于厚工件内的均匀残余应力也可采用该方式。

（3）如图4－1（b）所示，工件内的残余应力沿孔深方向的大小是变化的。本方法将其描述为阶梯状应力分布，在钻孔过程中每一个深度增量对应一个深度梯度。在第k个深度梯度内的平面应力为（σx）k，（σy）k和（τxy）k。可采用这种方式测量厚工件内的非均匀残余应力。

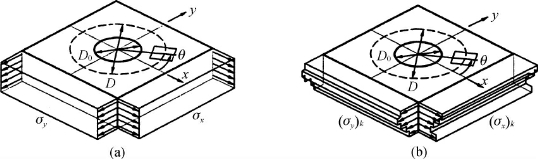
图4－1 钻孔尺寸与残余应力

2．应变花

如图4－2所示，一个应变花通常由两个或两个以上应变单元（敏感栅）组成，可将其粘贴在工件的特定位置。

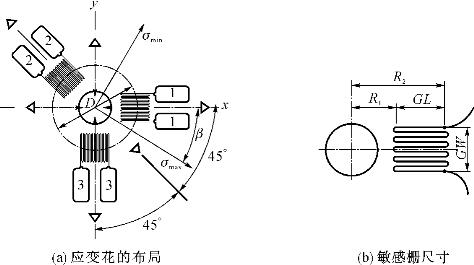
图4－2 典型三向应变花的布局与几何尺寸

应变花有三种类型，相关尺寸如表4－1所示。

表4－1 应变花尺寸单位：mm

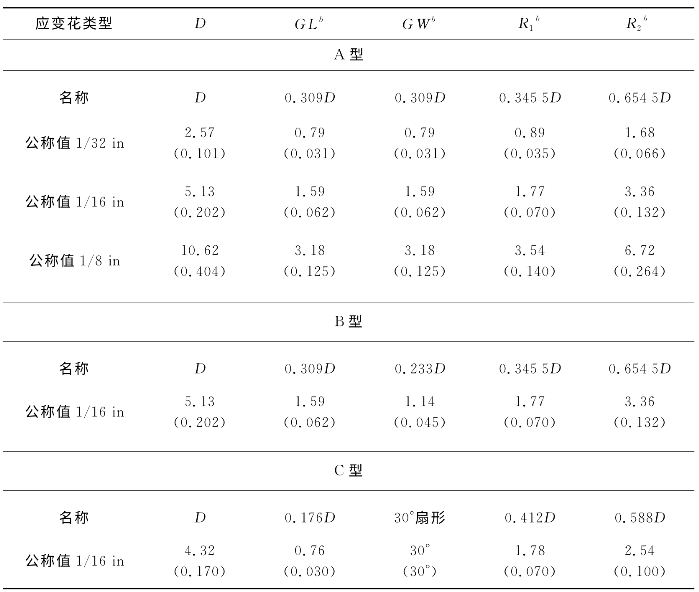
注：括号中数值为英寸；形状详见图4－2。

3．钻孔

（1）在应变花上分多步或一步进行钻孔。

（2）钻孔后，原先存在于所钻孔洞边界内的残余应力会得到部分释放，可采用合适的应变仪来测定钻到某一个指定孔深后所对应的释放应变。

4．残余应力计算方法(www.daowen.com)

1）一般要求

（1）采集钻孔后的释放应变并利用基于线弹性理论［2－5］的数学关系式可计算出原先在孔洞位置上的残余应力，释放应变的大小取决于孔内材料原始的残余应力。

（2）均匀应力情况如图4－1（a）所示，钻孔后测得的表面释放应变按式（4－1）计算：

2）方法A

（1）标定常数a和b表示在孔深范围内由单位应力所带来的释放应变，它们是无量纲的，其大小与材料无关。对于在较薄工件上的通孔以及较厚工件上的盲孔这两种不同情况，具体数值会略有差异。标准型应变花的具体标定常数已采用有限元方法计算获得，并在表4－2中列出。

（2）对于如图4－1（b）所示的非均匀应力情况，在完成第j步钻孔后所测得的表面释放应变实际上与之前1≤k≤j所有孔深状况下材料内（未得到完全释放）的残余应力相关，可按式（4－2）计算：

（3）标定常数矩阵和bjk表示当钻进到第j步孔深时，由于受到第k步孔深处的单位应力影响所引起的释放应变。图4－3列举了采用四步钻孔法时孔截面的一系列变化情况。在该系列中，当钻到第3步孔深时会受到第2步孔深处单位应力的影响，而标定常数矩阵所表征的就是这种过渡状态。标准应变花的标定常数已采用有限元方法［4］计算获得，具体数值可参考《金属材料 残余应力测定 钻孔应变法》（GB／T 31310—2014）中的表3。

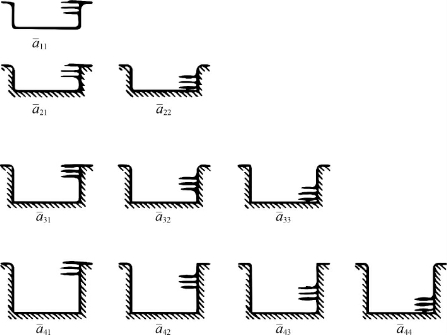
图4－3 标定常数矩阵的物理说明

（4）测量在一系列孔深阶段上的释放应变以提供足够的信息来计算每个阶段中的应力σx，σy和τxy。再根据这些应力来计算主应力σmax和σmin以及方位角β。

3）方法B

（1）标定常数与材料和钻孔刃具有关，标定常数需按低速钻孔标定实验方法确定。

（2）由于采用低速钻孔标定实验，无法控制步进孔深，一般均按均匀应力场处理，一次钻到最终深度。

（3）孔深的影响：释放应变的大小主要受近表面残余应力的影响，随着距表面深度的增大，内部应力的影响会逐渐消失。因此，方法B仅适用于近表面残余应力的评估，对较深部位的内应力无法给出可靠的测试结果。