目前，超声波检测对于平面应力场的研究大部分基于单向应力状态，少有考虑双向应力共同作用的情况［58，59］。对于金属材料实际状态存在复杂应力场的情况，若使用单轴应力状态下的应力系数，会使测量结果有偏差。为了正确地测量材料表面的应力分布，本研究采用航天结构常用的5A06铝合金作为被测材料，分别对单向和双向应力状态下的铝合金试件采用临界折射纵波法进行测试，得到单向和双向应力曲线，确定单向、双向应力状态下的应力系数。对比分析结果表明，单向加载条件和双向加载条件下的应力系数及应力数值存在差异。研究结果可为实际生产过程中的航天器铝合金残余应力的精确评估提供参考。

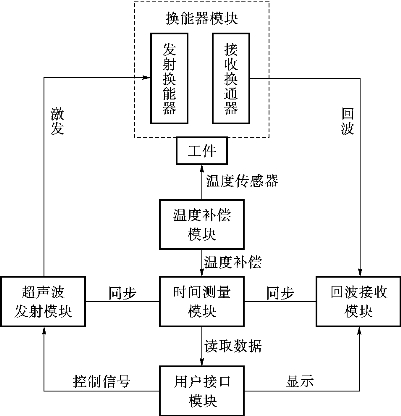
图2－11 LCR波残余应力检测系统框图

试验采用的LCR波残余应力检测系统框图如图2－11所示，共有6大模块。测量系统实物图如图2－12所示，探头频率为5MHz。双向加载采用平面双轴疲劳试验机（图2－13），极限拉伸载荷为250kN。

图2－12 超声波检测系统实物图

图2－13 平面双轴疲劳试验机实物图

为了更真实地标定应力系数，验证在标定应力系数过程中，与超声波传播方向垂直的应力是否对应力系数会有影响，设计可双向夹持的十字形双向加载试件。选择航天器常用的5A06铝合金材料，加工要求：平面度≤0．03、表面粗糙度≤6．4μm。为避免夹持端应力集中，试件4个夹持端之间用圆弧过渡连接。拟定试件中部200mm×200mm的区域为LCR波应力测量区。为了在弹性变形范围内获得尽可能高的加载应力，对该区域的厚度进行减薄处理，并在试件中心打孔。将LCR波换能器放置在中心圆孔和减薄区边缘的中间位置，即距离圆孔中心50mm处。试件的几何尺寸如图2－14所示。

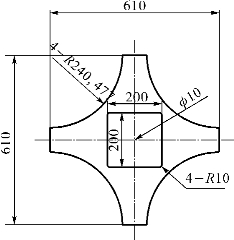
图2－14 双向拉伸试样尺寸图（单位：mm）

为验证试样设计的合理性，对试样受力情况进行仿真分析。分别采用壳单元和实体单元建模，得到厚度为4mm的实体单元建模应力分布图和法向应力分布图。

对于厚度为4mm的铝合金薄板，圆孔边缘的法向应力最大为42kPa，其等效应力为1．04MPa，法向应力占比为4．04%，如图2－15所示，可近似认为将薄板简化为平面应力状态。因此，模型采用壳单元，为平面应力状态。

仿真计算减薄处理到4mm的5A06铝板的应力集中点达到屈服状态（屈服应力取160MPa）时的加载力和应力分布，为进一步确定试验加载条件和应变片布置提供依据。采用壳单元进行建模，尺寸与试验件一致，网格密度为2mm，双向同时施加1kN的拉力，壳单元模型如图2－16所示。

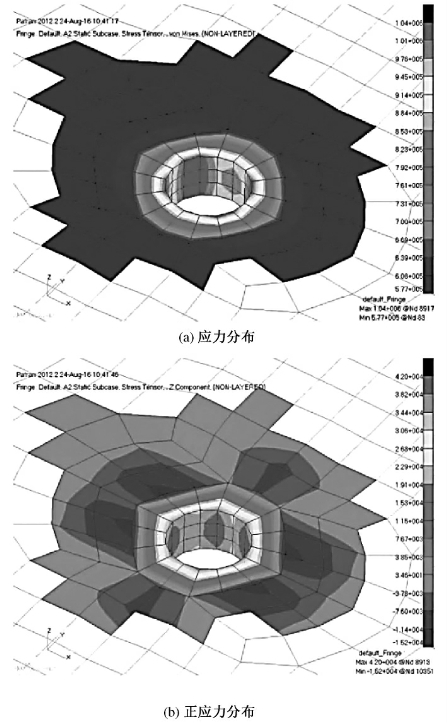
图2－15 厚度为4mm的圆孔边缘应力分布

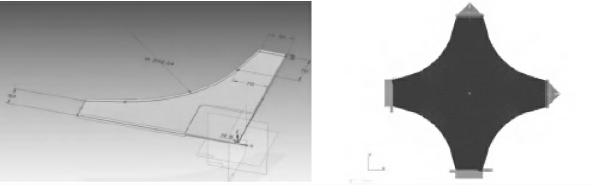
图2－16 壳单元模型图

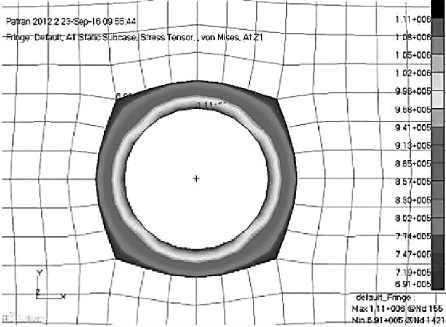
为研究减薄区域的应力分布，将应力集中区域放大（图2－17）。由于超声波检测的是其传播路径上的平均应力，故应将LCR波换能器放置在应力变化较小处。由图2－17可知，通过网格单元的初步估算，近似认为距离圆孔中心50mm的区域是应力均匀分布。因此，将LCR波换能器放置此区域，中心打孔区（直径10mm）的应力分布如图2－18所示。由图2－18可知，小孔边缘2mm（一个网格）以内区域存在应力集中，当在两端加载1kN的拉力时，最大应力为1．11MPa。当铝板中心圆孔边缘达到160MPa的临界屈服时，线性推算出双向加载的拉力最大为144．14kN。

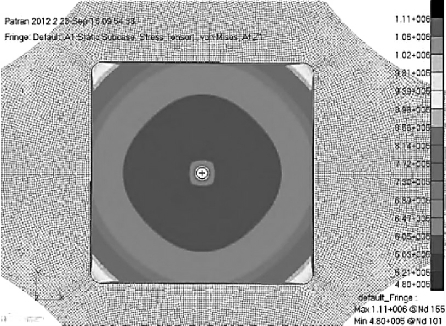
图2－17 LCR波测量区域应力分布图

(www.daowen.com)

图2－18 打孔区域应力分布图

在250kN平面双轴疲劳试验机上提供双向加载力，从10kN开始，以10kN递增，并以仿真结果作参考，在安全范围内考虑最大加载为110kN，以免铝合金薄板发生塑性形变。试验件背面贴8组应变片，加载过程中同步采集应变片应变数据，试验结束后通过应变计算应力值。贴好应变片的实物图如图2－19所示。

图2－19 应变片实物图

首先，沿B轴单向加载0～110kN的拉力，以10kN为步长，换能器平行于B轴放置。以应力为横坐标，声时差为纵坐标，获得应力与声传播时间变化量的关系（图2－20）。

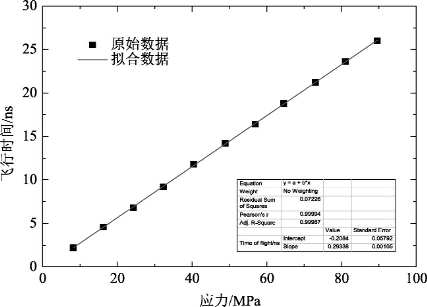
图2－20 平行加载方向的单向应力系数标定图

由图2－20可知，应力与声时差之间存在良好的线性关系，拟合得到单向应力系数k∥＝3．4MPa／ns。采用拟合数据k∥＝3．4MPa／ns，根据超声测量得到的声时差，计算得到超声波实测的应力值。

然后，沿A轴单向加载0～110kN，测量LCR波传播方向垂直于应力方向的单向应力系数，换能器平行于A轴放置，步长为10kN。以应力为横坐标，声时差为纵坐标，得到临界折射纵波传播时间与垂直方向加载条件下应力的关系。

由图2－21可知，应力与声时差之间存在良好的线性关系，得到垂直加载方向的单向应力系数k⊥＝11．24MPa／ns。分析图2－20、图2－21可知，平行加载方向的应力系数k∥＝3．4MPa／ns，而垂直加载方向的应力系数k⊥＝11．24MPa／ns，说明LCR波的传播时间变化量受不同方向应力的影响而出现明显差异。垂直应力方向的声弹性效应约为平行方向的33%。

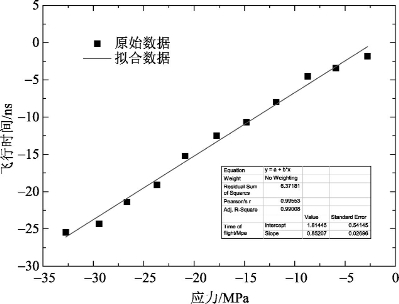
图2－21 垂直加载方向的应力系数标定图

取拟合数据k⊥＝11．24MPa／ns，根据超声测量得到的声时差，计算超声波实测的应力值，以拉力值为横坐标，分别以应变片计算的应力值和超声测量应力值为纵坐标，获得垂直加载方向的应变片测量计算的应力与超声测量应力对比关系（图2－22）。由图2－22可知，二者斜率只相差0．141，近似相同，只是截距有1．801 5的差距，说明标定的平行加载方向单向应力系数线性度良好。实验得到的超声测量结果与应变片计算的应力值最大偏差小于5MPa。

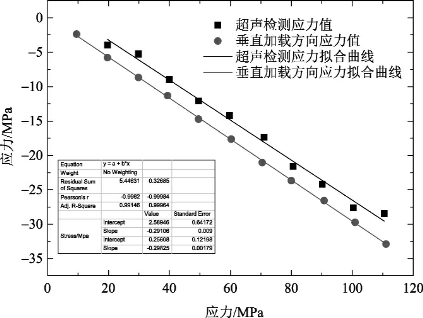
图2－22 垂直加载方向的应变片应力值与超声测量应力对比图

在A，B双向拉伸加载相同载荷的条件下，测量LCR波双向应力系数，以应力为横坐标，声时差为纵坐标，进行曲线拟合，结果如图2－23所示。

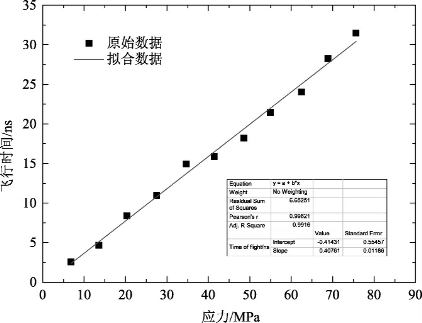
图2－23 平行加载方向测量的双向应力系数标定图

由图2－23可知，应力与声时差之间存在良好的线性关系，拟合得到双向应力系数kB＝2．44MPa／ns。根据超声测量得到的声时差，计算得到超声波实测的应力值。

比较图2－20、图2－23的应力系数，双向加载情况下和单向加载情况下不同，这说明垂直方向的应力对应力系数有一定程度的影响。双向加载情况下得到的应力系数为2．44MPa／ns，即2．44MPa的应力就可以引起1ns的声时变化，相比单向加载时的3．4MPa，双向加载引起1ns的声时所需的应力小了0．96MPa，说明双向加载情况下，垂直与平行方向的应力共同作用引起声时变化，垂直方向应力的作用约为平行方向应力的33%。