纳米压痕技术是在Hertz理论基础上形成的，测量得到的应力为接触附近区域的应力大小［2］。压痕过程分为加载和卸载两个阶段。加载时，压头压入样品表面，材料发生弹性和塑性变形。在卸载过程中，如果材料的弹性位移得到恢复，则可通过对卸载曲线分析得到材料的硬度及弹性性能［3，4］。图2－1为典型的载荷－位移曲线图，图2－2为压痕卸载后的各参数示意图。

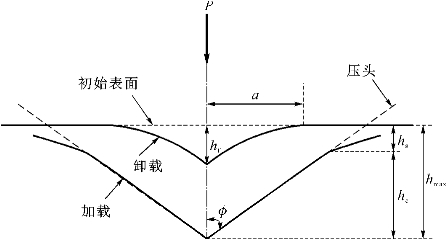
图2－2 压痕试验材料卸载后的参数示意图［4］

目前，压痕仪可控制载荷发生连续变化，实现对压入深度的在线测量，加之纳米压痕过程中施加的是超低载荷，可以获得纳米级的压深，可对薄膜材料的力学性能进行测试。图2－2中hmax为最大压入深度，hc和hf分别为最大接触深度和塑性深度，hs为材料表面接触周边的偏离高度，其中，h，hf可直接从载荷－位移曲线中直接得到，hc，hs可通过式（2－1）和式（2－2）计算得到［5］。

接触深度hc可由以下公式计算得出：

式中 ε——与压头形状相关的参数，其中锥形压头ε＝0．72；

hs——表面接触周边的偏离高度；

Pmax——最大压入载荷；

S——材料的接触刚度。

式中，hmax为压头压入的最大深度。

对载荷－位移曲线卸载部分进行拟合，建立卸载位移与载荷的关系［5］。

式中 hf——完全卸载后残留深度；

B，m——可通过测试获得的拟合参数，对Berkovich压头，m值介于1．2～1．5之间。

采用最小二乘法对载荷－位移曲线卸载曲线顶部25%～50%的部分进行拟合，得到材料的弹性接触刚度［6，7］：

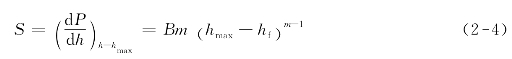(www.daowen.com)

压痕接触面积可根据经验公式计算得到［8］：

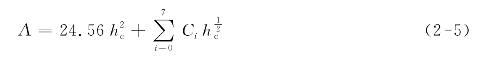
式中，Ci为常数，压头不同，其数值则不同，该值由试验确定。

纳米压痕硬度的计算方法主要是Oliver－Pharr［9］法。计算公式如下［10］：

式中 Pmax——最大压入载荷；

A——有效接触面积。

因压头不是完全刚性体，Oliver－Pharr提出复合响应模量参量，对材料弹性接触刚度S的计算公式改进如下：

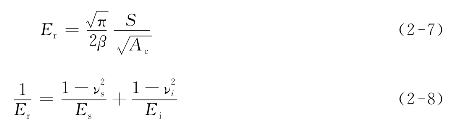
式中 β——数值与压头形状有关，对Berkovich压头来说，β＝1．14；

Ac——压头的有效接触面积；

νi——压头的泊松比；

νs——被测材料的泊松比；

Ei——压头材料的弹性模量；

Es——被测材料的弹性模量；

Er——通过试验求得复合响应模量。