由于应力集中,结构中的缺口部位有可能因服役载荷作用而引入残余应力。一般来说,这些应力对于裂纹形核、疲劳寿命、疲劳损伤等都很重要。如果发生塑性变形,缺口周围的残余应力的解析计算几乎是不可能的。这些计算可以采用有限元技术,尽管它们不能归入简单计算之列。我们可以通过一个基于诺依勃(Neuber)假设[3]的简单步骤,对σpeak作出合理的估计。只要不发生塑性变形,所有的应变都与施加的载荷成正比,服从胡克定律,应力和应变分布的形状与载荷无关。但是只要缺口根部产生塑性区,二者分布的形状就将变化。缺口根部应力(σpeak)低于弹性预测值,如图1-10(a)所示,并且同一位置的应变(εpeak)高于弹性预测值,如图1-10(b)所示,可用式(1-5)表达。

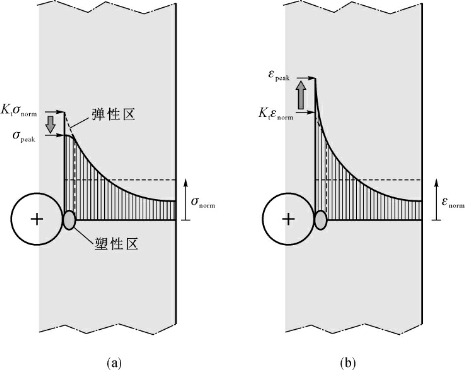
图1-10 由于缺口根部塑性区导致的应力与应变分布的差异
缺口根部应力(σpeak)低于弹性预测值这个事实,与另一个事实应变εpeak高于弹性预测值是互相联系的。根据Neuber假设,它们的乘积σpeakεpeak仍然符合弹性预测值[4]:
![]()
这意味着,在二者的乘积中,小于预测的σpeak被高于预测的εpeak所补偿。定义塑性集中系数Kσ和Kε为

Neuber假设就成为(https://www.daowen.com)
![]()
Neuber证明了,对于剪切载荷作用下的双曲线形缺口,他的假设是正确的。于是他假定,对于其他类型的缺口和载荷这个假设也将是近似正确的。这或多或少已经得到经验验证,前提是塑性区要小。
将εnorm=σnorm/E代入式(1-6),得到:

对于给定的载荷和Kt,式(1-9)右边是已知的常数值,因此该公式给出两个未知量(即σpeak和εpeak)之间的一个关系(双曲线)。为了确定σpeak和εpeak,需要有第二个关系,为此采用了从拉伸试验获得的材料应力-应变曲线。有了这两条曲线,图解法就如图1-11所示的那样简单。图中两条曲线的交点A所对应的σpeak和εpeak值满足这两个关系。如果不产生塑性变形,峰值应力σpeak应在B点。A点和B点的差值给出了峰值应力的下降量。弹性载荷卸载后,残余应力为
![]()
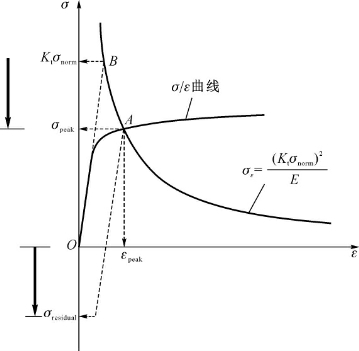
图1-11 确定 和
和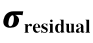 的图解法
的图解法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






