1.氢化反应以及动力学过程

金属与合金的氢化反应一般由以下几个步骤组成^[6]，如图8-1所示：

步骤1 氢气由气体主相向金属与合金迁移；

步骤2 氢气由气体相边界向金属与合金表面扩散；

步骤3 氢气在金属与合金表面形成物理态吸附，此时氢在金属合金表面的状态为氢分子；

步骤4 氢分子在表面分解形成氢原子，这些氢原子在金属合金表面形成化学态吸附；

步骤5 化学吸附在表面的氢原子穿透金属与合金的表面进入其主体；

步骤6 氢原子在形成的氢化物相中向颗粒内部扩散，到达氢化物与金属合金的界面；

步骤7 氢原子在氢化物与金属表面参与反应，形成氢化物。

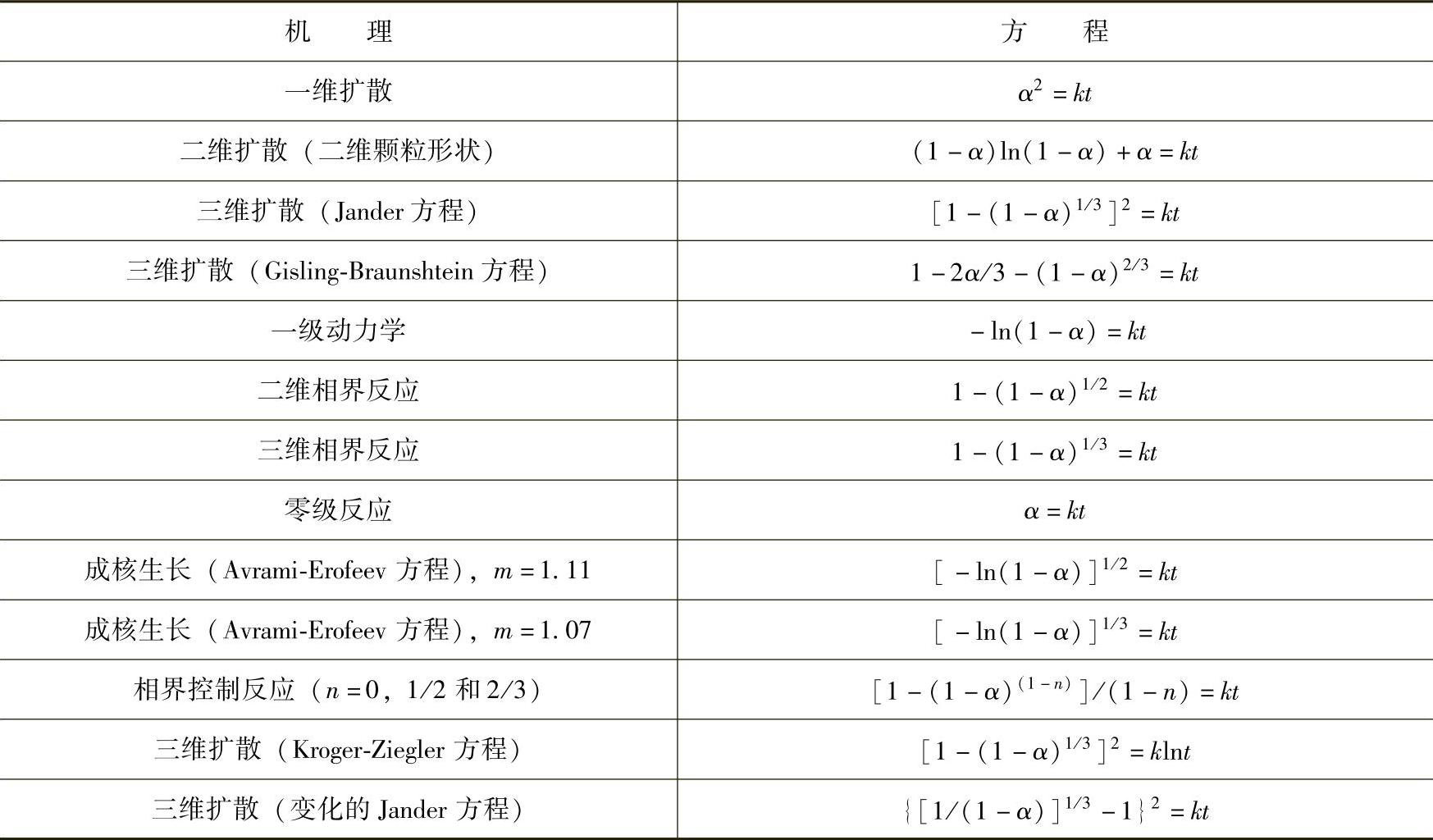
以上是简化的金属合金体系中的氢化反应过程，当体系是多元组分，或者有催化剂等其他因素时，氢化反应过程往往要复杂得多。在以上简单氢化反应过程中，一般步骤3～7相对于步骤1或者步骤2要慢得多，当其中某一个步骤是整个氢化过程中最慢的一步，整个反应的速度就由这个步骤决定时，此步骤反应称为氢化过程中的限速反应。很多人通过简易球形模型来研究不同储氢金属合金体系氢化动力学过程^[7-14]。根据不同的反应过程机理，不同的方程被用来解释这些反应过程（见表8-3），因此当氢化反应过程可以被某个方程很好地吻合时，即表明此方程所阐述的反应过程即为整个氢化反应过程中的限速反应。周国治等人引进了特征时间的概念，将合金吸氢百分数表达为时间、温度、压力、颗粒的函数的周氏动力学模型^{[6，11，12]}。

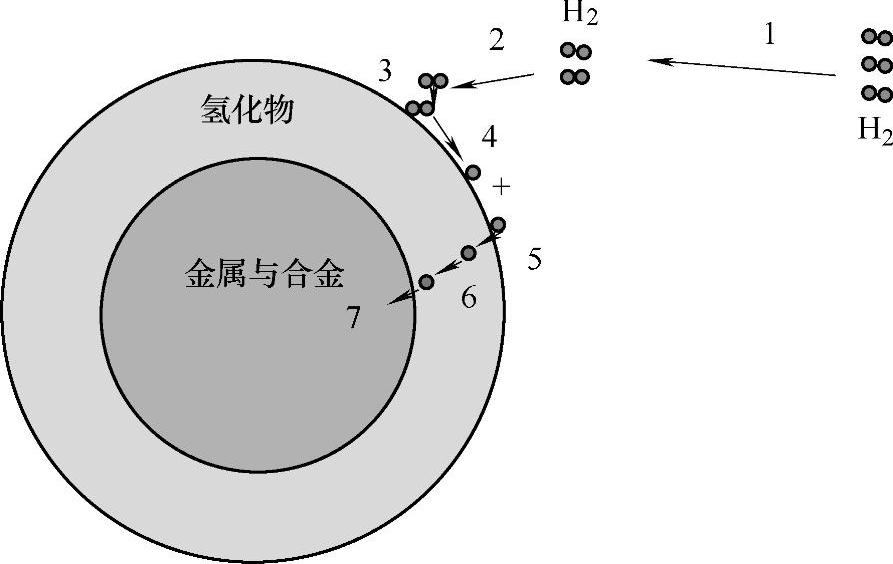
图8-1 金属与合金的氢化反应过程

表8-3 不同反应机理以及对应的反应方程

2.氢在金属中的扩散

氢原子直径较小，氢在金属中比任何其他溶质都扩散得快，在金属点阵内可以以很高的速度扩散，扩散系数通常在10^-8～10^-3cm²/s范围内，但对这种快速扩散机理还不完全清楚。氢原子的质量很小，可以预料量子效应和隧道效应起作用，氢在Nb、Ta和V等金属中扩散的活化能是同位素质量函数的事实支持了这种推测。研究氢在金属中的扩散行为是确定氢在金属中行为的一个很重要的方面，尤其是对于储氢合金体系中的氢扩散研究，对于吸放氢过程中的动力学有很大的影响。氢在金属中扩散系数的测定方法可以使用核磁共振法、弹性后效法等，在金属体系中氢浓度很高时，可以采用穆斯堡尔谱法及中子衍射等方法来测定。但不同人测得的氢扩散数据有的可以相差达几个数量级，原因之一是氢扩散实验的结果受样品表面状态的影响很大。另一重要原因是氢在金属中的扩散系数与金属本身的纯度等因素关系很大，当金属中存在O、N等杂质原子后，这些原子对氢原子具有明显的俘获作用，从而可能大大降低氢的扩散系数。

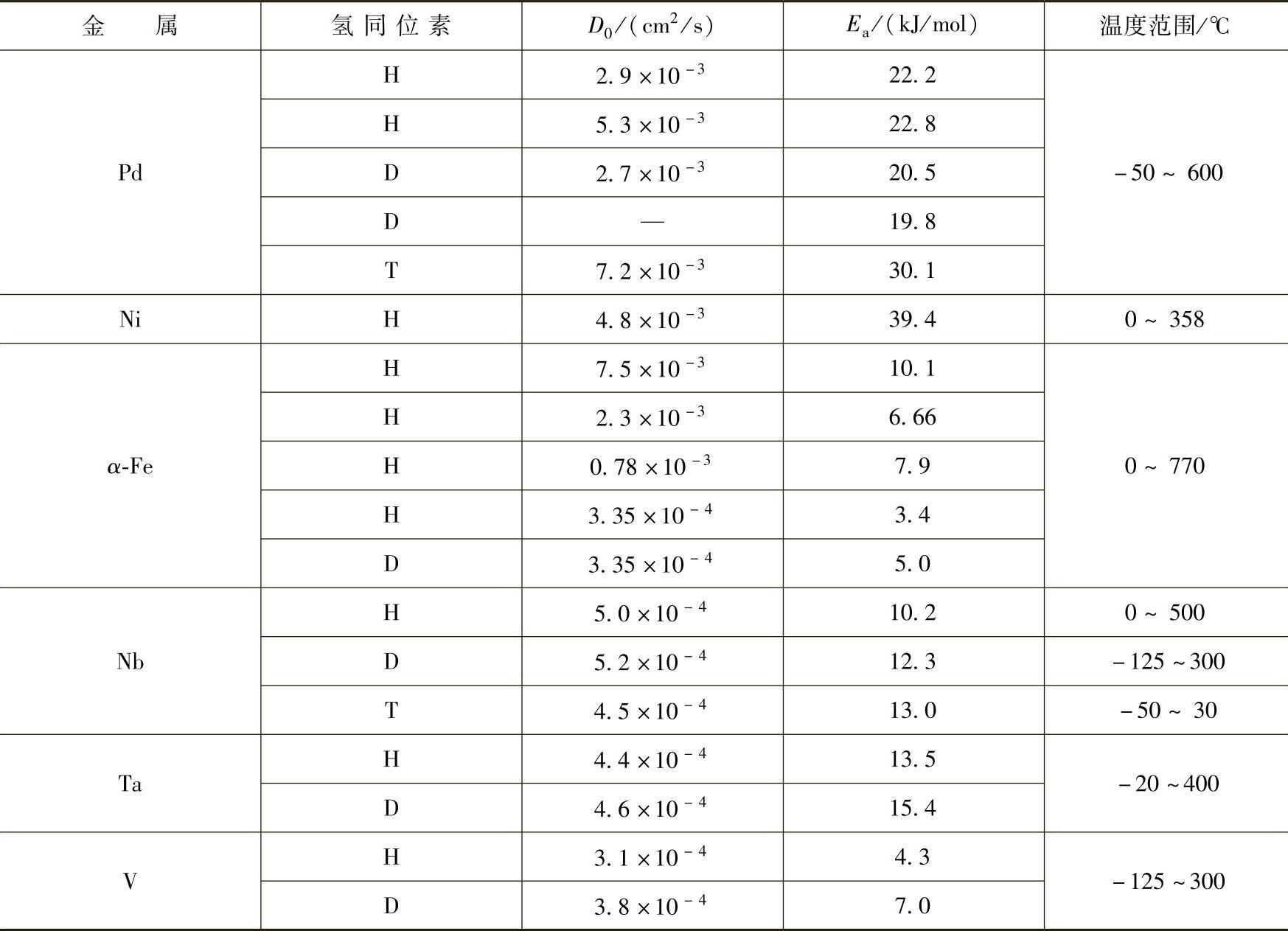
Kehr认为氢在金属中有4种可能的扩散机理^[15，16]。如图8-2所示，在极低的温度下，氢作为带态而形成离域化，在带态中的氢的传播受到声子和晶格缺陷散射的限制。在稍高的温度下，氢被定域在具体的间隙位中，需要热能来改变其位置。这时分两种情况，一种可能性是从一个间隙位跳到另一个间隙位的隧穿。另一种可能性是在两个位间的跳跃，这便涉及氢扩散的活化能，这是经典的扩散机制，在高温时起主要作用。在极高的温度下，氢在高于势垒的态上，此时的扩散与稠密气体和液体中的一样。表8-4^[16]显示了低浓度的氢同位素在各种金属中的扩散系数，用Arrhenius方程D=D₀exp（-E_a/RT）中的指前因子D₀与活化能E_a表示，其中D（cm²/s）为扩散系数，D₀称为扩散常数，E_a为氢的扩散活化能，R为气体常数，T为绝对温度。

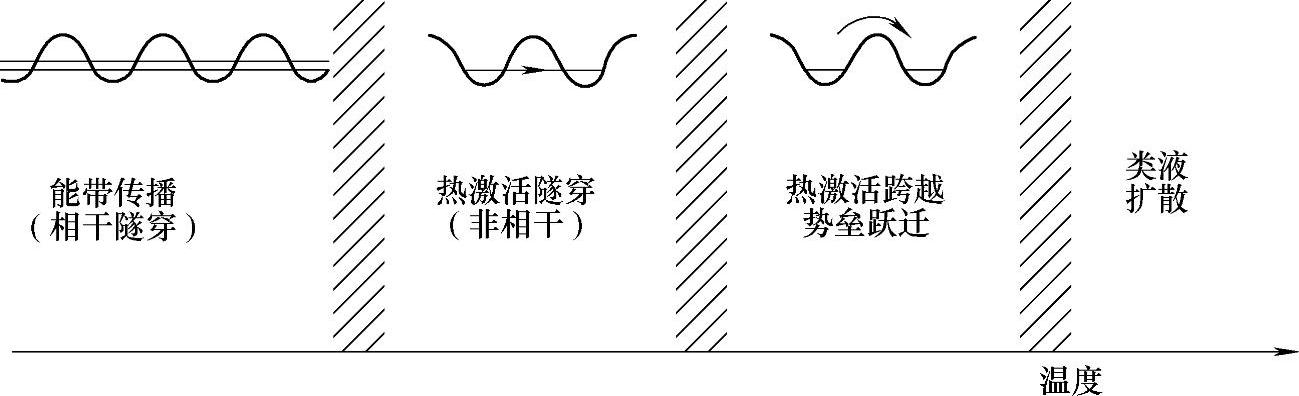
图8-2 不同温度下氢在金属中的4种可能的扩散机理

表8-4 低浓度氢在不同温度下不同金属中的扩散系数及活化能

3.金属合金氢化反应化学与热力学原理

在一定温度和氢气压力条件下，储氢金属或合金与氢反应生成金属氢化物，并释放出热量，当提高温度或降低氢气压力时，氢化物释放出氢气，可以用式（8-1）表示。(www.daowen.com)

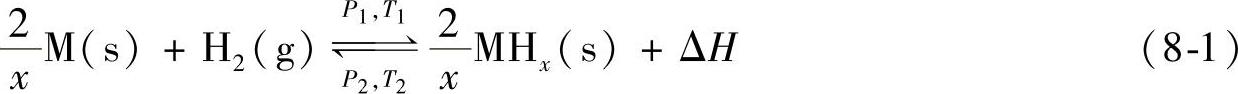
M代表金属和合金，ΔH为反应热，P₁、T₁和P₂、T₂分别表示吸收和放出氢时压力和温度条件。正向反应为吸氢，逆向反应为放氢，这样我们便可以通过控制和调节体系的温度和氢气压力来使得金属和合金氢体系吸收和放出氢，这便是储氢金属和合金吸放氢的基本原理。这样的反应可以直观地通过储氢合金与氢反应的平衡压力-组分-等温（PCT）曲线图来显示。图8-3显示的为一典型的吸氢过程PCT曲线图，横轴表示的为合金中的氢的含量，通常以氢原子与金属原子的比值表示，纵轴表示的为氢的平衡压力，一般以对数形式显示。

从图中A点开始，氢气分子在金属表面离解为氢原子，氢原子从金属表面扩散进金属内部，进入金属晶格的间隙，形成氢-金属固溶体，从A点走向B点，这时的金属称为α相（即AB段）。从B点开始，此时氢开始与金属反应，生成氢化物，从B点走向C点，这时生成氢化物β相，因此，BC段为α相和β相共存相。根据Gibbs相律F=C-P+2，在BC段，C只有金属和氢，P为α相、β相和氢气，所以F=2-3+2=1，组分发生改变时，平衡压力不改变，所以BC段理想状态时为平的台阶。C点以后，α相消失，此时压力再升高时，氢化物中的氢含量有少量增加，直至到达D点，最终氢化反应结束。图8-4显示不同温度下测量得到的PCT曲线，然后通过这些曲线得到van't Hoff曲线方程，从而得到反应焓和反应熵的示意图^[17]。一般随着温度的升高，体系的氢平衡压逐渐提高，同时在热力学控制下，平台区也逐渐缩短。从PCT曲线上，我们可以了解金属（合金）与氢反应时的平台压力、最大吸氢量、平台宽度（为有效放氢区间）、滞后效应等衡量储氢材料性能的一些重要指标。

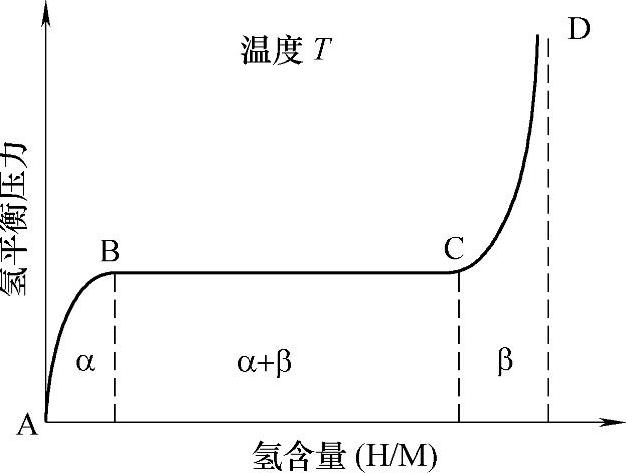
图8-3 吸氢过程的压力-组分-等温（PCT）曲线图

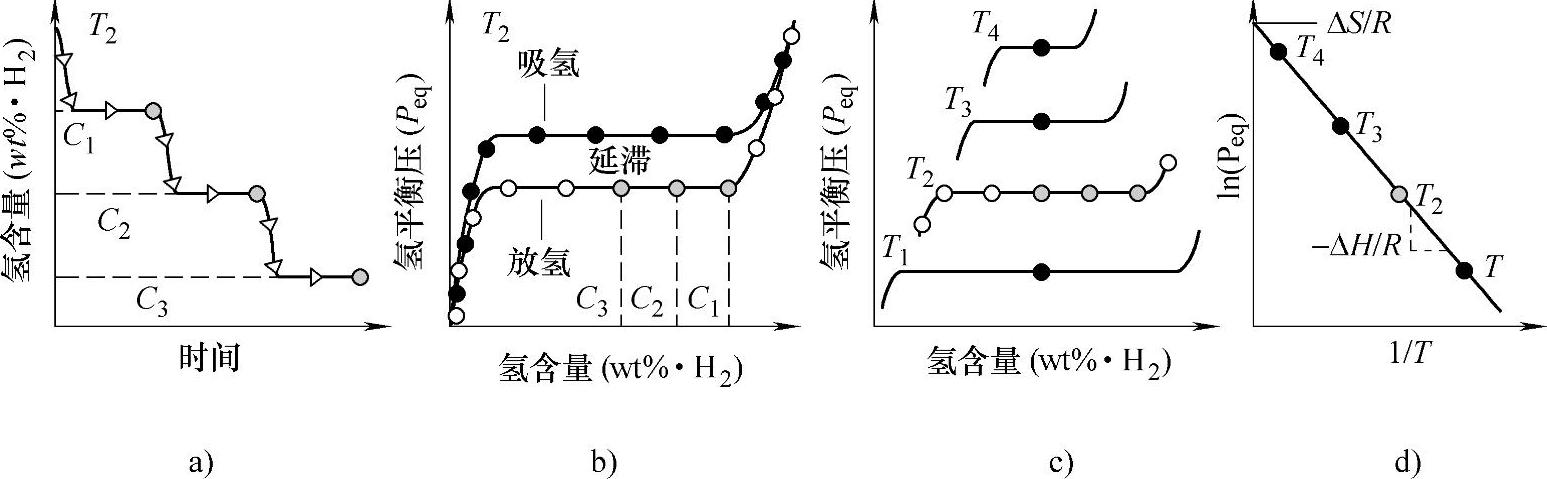
图8-4 通过PCT温曲线测量来计算热力学性能

a）组分随时间的变化 b）吸氢和放氢过程PCT曲线 c）不同温度放氢曲线图，温度大小T₁＜T₂＜T₃＜T₄ d）通过van't Hoff曲线计算放氢过程反应焓（生成焓的相反值）和放氢过程反应熵（生成熵的相反值）

根据方程式（8-2）和方程式（8-3），我们可以推导出van't Hoff方程式（8-4）。

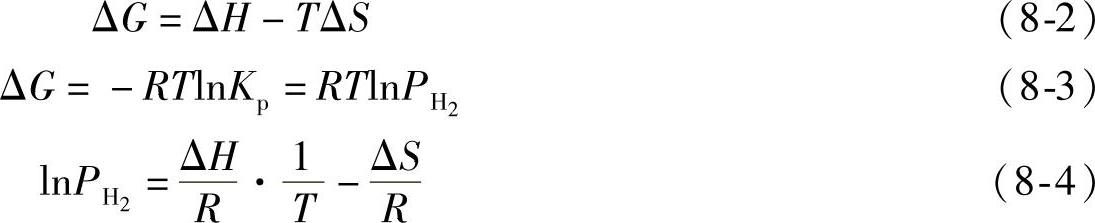
式中，ΔG，ΔH和ΔS分别为反应的Gibbs自由能的变化量、焓变化量以及熵变化量；K_p为平衡常数；R为气体常数；T为热力学温度，单位为K。

根据PCT曲线中得到的不同温度下的放氢平衡压，我们便可以得到表示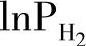与1/T关系的van't Hoff曲线图，并拟合出此反应的van't Hoff方程。根据方程的斜率和截距，我们可以分别得到氢化物的反应生成焓和生成熵。图8-5为几种常见金属体系的van't Hoff曲线图^[18]。从不同体系的van't Hoff曲线图上，我们可以直观地挑选出我们所需要的在不同温度和压力条件下能够释放氢的体系。由图8-5我们也可以看出，目前使用广泛的LaNi₅的氢化物在室温附近就能够在比较合适的压力下释放氢。

4.氢在储氢金属合金中的位置

中子衍射已经证实，传统的储氢合金与氢反应形成间隙型氢化物时，氢进入合金中的晶格间的位置里，一般填充在金属晶格的四面体或八面体的间隙位置上。典型的金属晶格有面心立方（fcc）、体心立方（bcc）以及六方密堆积（hcp）。图8-6显示的为氢原子占据金属晶格中的四面体或八面体的间隙位置^[19，20]。

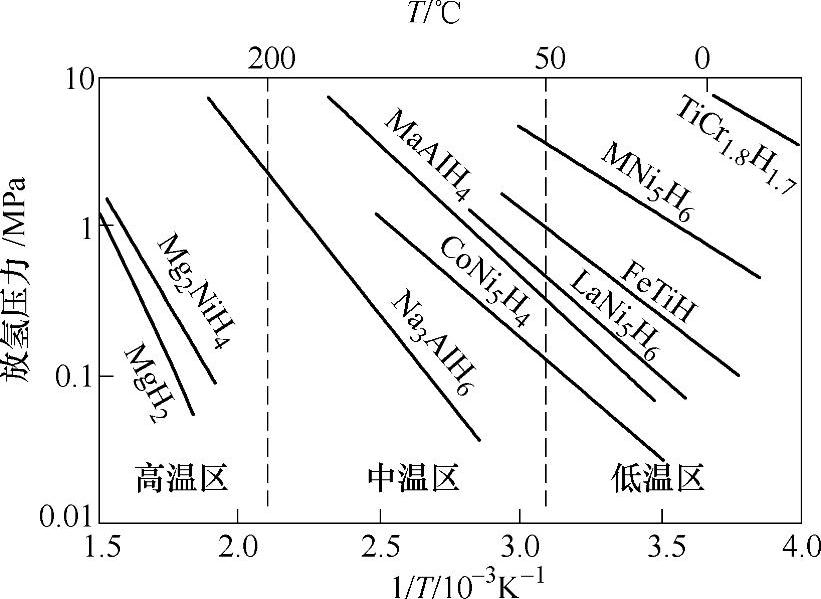
图8-5 常见金属体系的van't Hoff曲线图

图8-6 氢占据金属中四面体（T）或者八面体（O）间隙位置

当氢占据不同金属晶格的不同间隙位置时，每个金属原子可以被占据的氢原子数分别为：fcc晶格中，八面体位置1个，四面体位置2个，bcc晶格中，八面体和四面体的位置分别为3个和6个，而hcp中对应的分别为1个和2个（见表8-5）。我们可以看到bcc结果晶格相对于fcc和hcp结构，单位金属原子可被占据的间隙位置大大高于其他金属，这表明bcc结构在储氢材料领域可能具备独特的性能应用。比如bcc金属V或者bcc结构Ti-V基合金等，如果氢能够占据所有的四面体和八面体空隙，其储氢容量将可以达到15%左右（对于VH₉），不过由于一般氢原子在金属态氢化物中相互距离要大于2.1Å等规则^[21，22]以及电子化学结构等方面的限制，使得氢在金属与合金中往往只部分占据某种间隙。

表8-5 不同结构金属的八面体和四面体间隙