氢气在高温低压时可看做理想气体，通过理想气体状态方程PV=nRT来计算不同温度和压力时的质量。然而，由于实际气体分子体积和分子相互作用力的原因，随着温度的降低和压力升高，氢气越来越偏离理想气体的性质，范德瓦尔斯方程不再适用。实际气体与理想气体的偏差在热力学上可用压缩因子Z表示，定义为Z=PV/nRT。图5-1列举出几种气体在0℃时压缩因子随压力变化的关系。从图可以看出氢气的压缩因子随压力的增加而增大。

为正确地描述真实气体的性质，历史上曾提出过许多真实气体的半经验方程，著名的如范德瓦尔斯方程、彭-鲁滨逊状态（P-R方程）、R-K方程、贝蒂一布里奇曼方程、BWR方程、M-H方程等。这些方程的形式一般由理论分析得到，方程中含有两个或多个与计算气体相关的常数，适用于不同的气体。此外，根据对比态原理又发展了各方程的对比态形式，此时方程中的常数不再随气体的不同而不同，而是为一定压力温度范围内的同类气体通用。

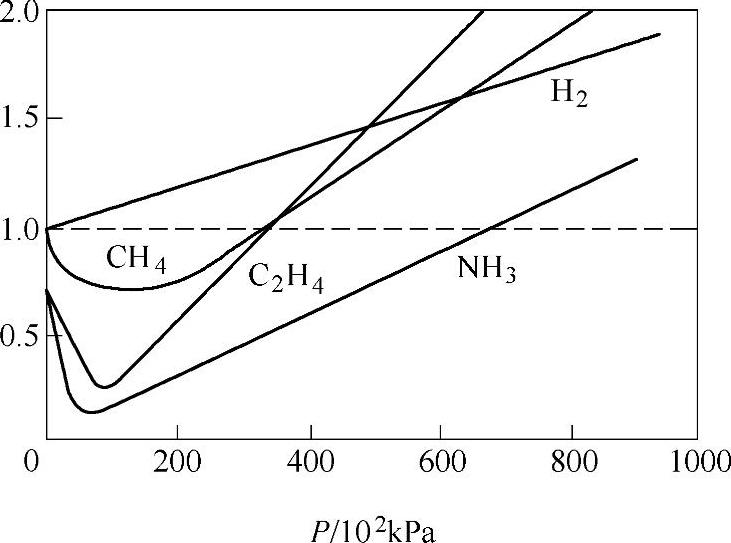
图5-10 ℃时几种气体的Z-P曲线(www.daowen.com)

通过美国国家标准技术所（National Institute of Standard sand Technology，NIST）材料性能数据库提供的真实氢气性能数据进行拟合，可得到简化的氢气状态方程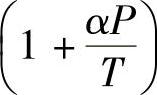：，其中，α=B₁=1.9155×10^-6K/Pa^[1]，在173K＜T＜393K范围内计算，最大相对误差为3.80%；在253K＜T＜393K范围内计算，最大相对误差为1.10%。图5-2比较了几个不同状态方程计算的不同温度下氢气压力和密度的关系。

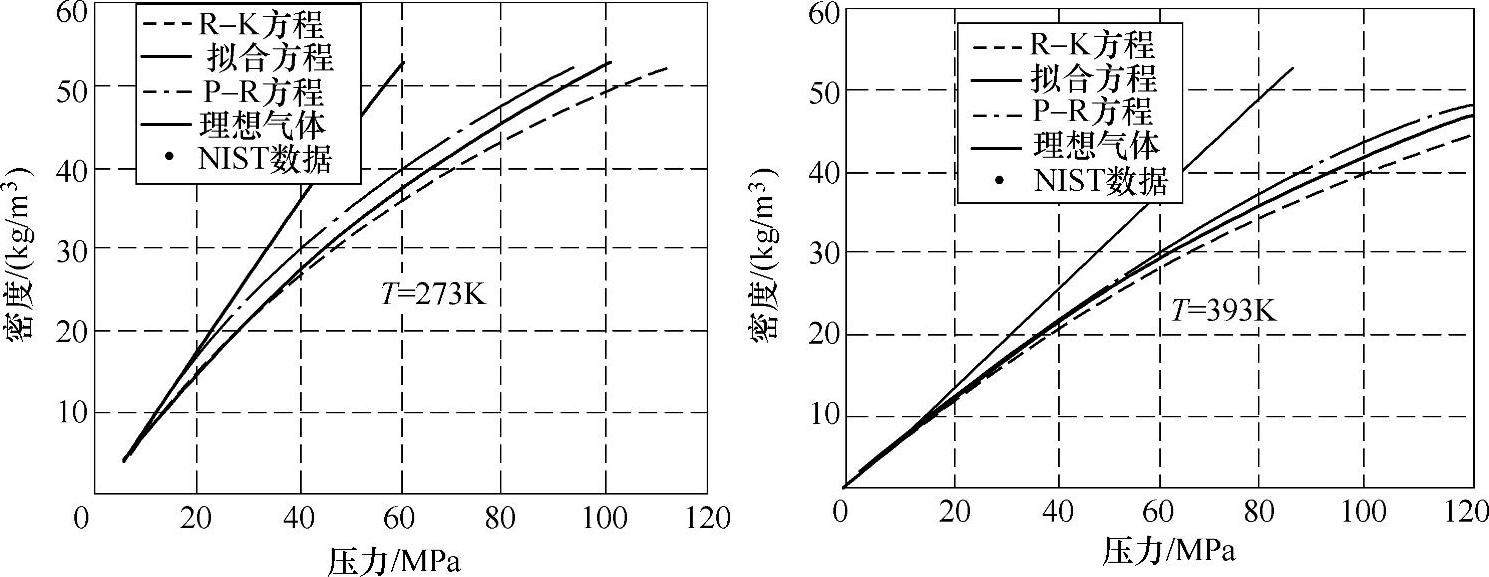
图5-2 T=273K、393K时氢气压力和密度的关系