1.H₂的分子结构

H₂是最简单的双原子分子，其成键模型可以简单描述为两个氢原子各提供一个电子，形成一个共价键，两个电子自旋相反，因此H₂呈抗磁性。从核间距——势能图（见图2-2）中可以看出，在两个电子自旋相反的条件下，两个氢原子构成的体系能量在某一特定的核间距下达到最小值。H₂分子中两个氢原子平衡距离为0.74611 Å^[2]，键能为4.52eV。

分子轨道的观点认为，在形成H₂分子时，两个H原子的1s轨道的波函数通过线性组合，得到了两个分子轨道，即

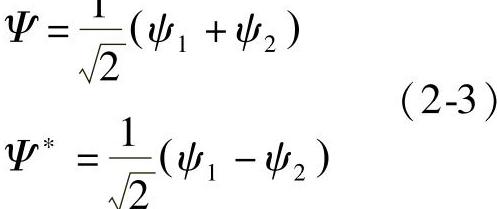
式中，ψ₁和ψ₂代表两个氢原子1s轨道的波函数；2^-1/2为归一化因子；Ψ称为成键轨道，由两个原子的波函数同相位叠加获得，为反演对称结构，其能量低于未成键的原子轨道；Ψ^*称为反键轨道，由两个原子的波函数反相位叠加获得，为反演反对称结构，其能量高于未成键的原子轨道。

H₂分子中的两个电子在重新组合得到的分子轨道中按照能量的高低排布，这种排布与电子在原子轨道中的排布类似，同样符合Pauli不相容原理和Hund规则，即不存在两个状态完全相同的电子，因此每个分子轨道至多能排布两个电子，而当存在能级相同的简并轨道时，电子倾向于以自旋相同的方式分占不同的轨道。对于H₂来说，两个电子同时占据成键轨道，因此获得了净的能量，即为H-H键的键能。两个H原子形成H₂分子轨道的示意图如图2-3所示，其中σ、u、g均为分子对称性的标识，σ表明键具有旋转对称性，u和g分别表示反演反对称和反演对称。

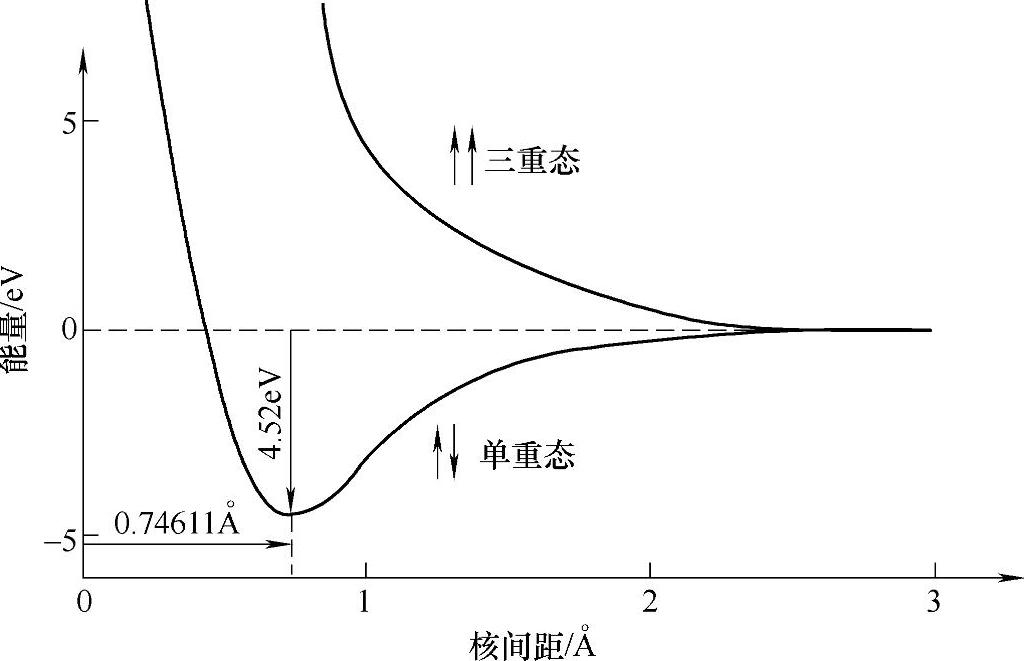
图2-2 H₂分子的核间距——势能图

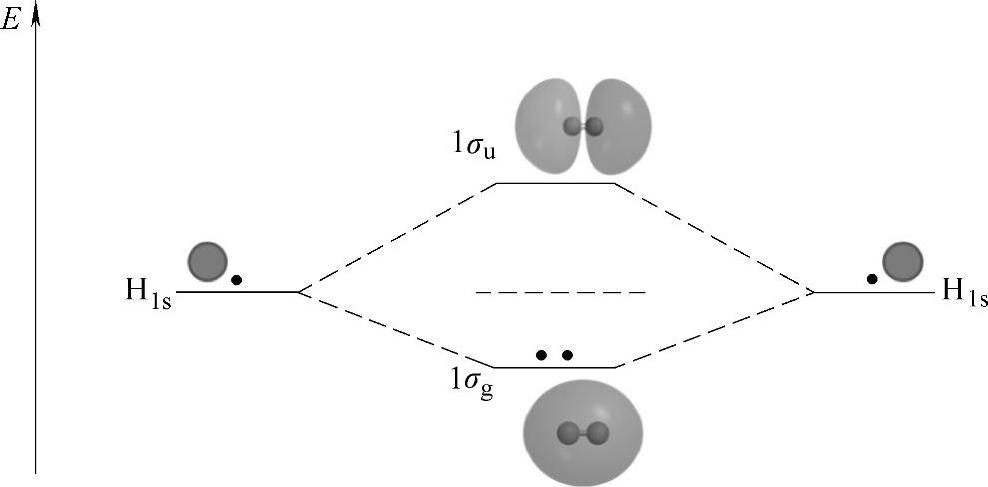
图2-3 H₂的分子轨道示意图

对于H₂这样的简单分子，经典的化学键理论和基于量子化学原理的分子轨道理论都能很好地描述其结构。但分子轨道理论将分子作为一个整体来处理，能较好地解释一些传统化学键理论不能很好解释的结构和现象，例如H₂分子作为一个配体对过渡金属原子进行配位以及过渡金属对H₂分解的催化机理等，在后面讨论氢的化学反应和成键时会看到分子轨道理论更多的应用。

2.氢气的核自旋异构体^[1]

与电子自旋类似，原子核同样具有自旋。¹H原子核中仅有一个质子，因此核自旋量子数S=1/2。当构成双原子分子时，核自旋有两种可能的组合：即两原子核自旋相同，此时整个H₂分子的自旋量子数为1/2+1/2=1，分子为三重态，称为正氢（orthohydrogen）；或两原子核自旋相反，此时整个H₂分子的自旋量子数为1/2-1/2=0，分子为单重态，称为仲氢（parahydrogen）。

这两种氢分子在能量上略有差别，通常的氢气是这两种核自旋异构体的混合物，常温常压下正氢能量较低，在273K下正氢约占75%；而在低温下仲氢更为稳定，接近0K时几乎所有的H₂均为仲氢。极限高温下两种核自旋异构体的比例可以从它们的统计权重得出：每个¹H原子有两种核自旋状态，组成H₂分子后分子的核自旋状态数为4，在这4种状态中，通过原子间波函数组合可以得到其中3种具有反演对称结构，属于正氢，一种为反演反对称结构，属于仲氢。因此在高温极限下正氢的比例应为75%，在0℃时的分布已经十分接近这一极限值，表明两种异构体之间的能级差很低，但是在近室温下的转化比较缓慢。已发现顺磁性的气体分子如NO、NO₂等能有效地促进两种异构体之间的转化，而反磁性气体如N₂、CO₂等都没有效果，溶液中的顺磁性离子也对转化有催化作用。这两种氢气在物理性质如蒸气压、三相点等以及振转光谱的性质上略有差别。

这种核自旋异构体在原子核自旋不为0的双原子分子中是十分普遍的，氢的3种同位素构成的双原子分子均有核自旋异构体。D的核自旋量子数为1，因此有3种核自旋状态，D₂有9种核自旋状态，经分析其中6种为对称结构，3种为反对称结构，因此在高温极限下正氘和仲氘比例为2∶1。T与H一样核自旋为1/2，因此正T和仲T的高温极限比例也是3∶1。

3.氢气的物理性质

H₂是最轻的气体，汉语中的“氢”即取此意。利用其低密度，人们早在飞机发明之前就用氢气球实现了飞翔的梦想。1783年Jacques Charles首先发明了氢气球，1852年Henri Giffard发明了由氢气球作浮力的飞行器，后由德国人Ferdinand von Zeppelin改进得到了Zep-pelin飞艇，于1900年首次试飞，在1910～1914年间安全运送了35000多位乘客。氢气飞艇在第一次世界大战时用作空中的观察和投弹。直到1937年H₂飞艇发生空中燃烧爆炸的事故人们才逐渐停止使用H₂飞艇而转为更安全的氦气。

由于氢气的分子量是所有气体中最低的，因此具有所有气体中最高的热导率和扩散系数。氢气的主要物理性质见表2-4，其中列出了两种核自旋异构体的信息。

表2-4 氢气的主要物理性质

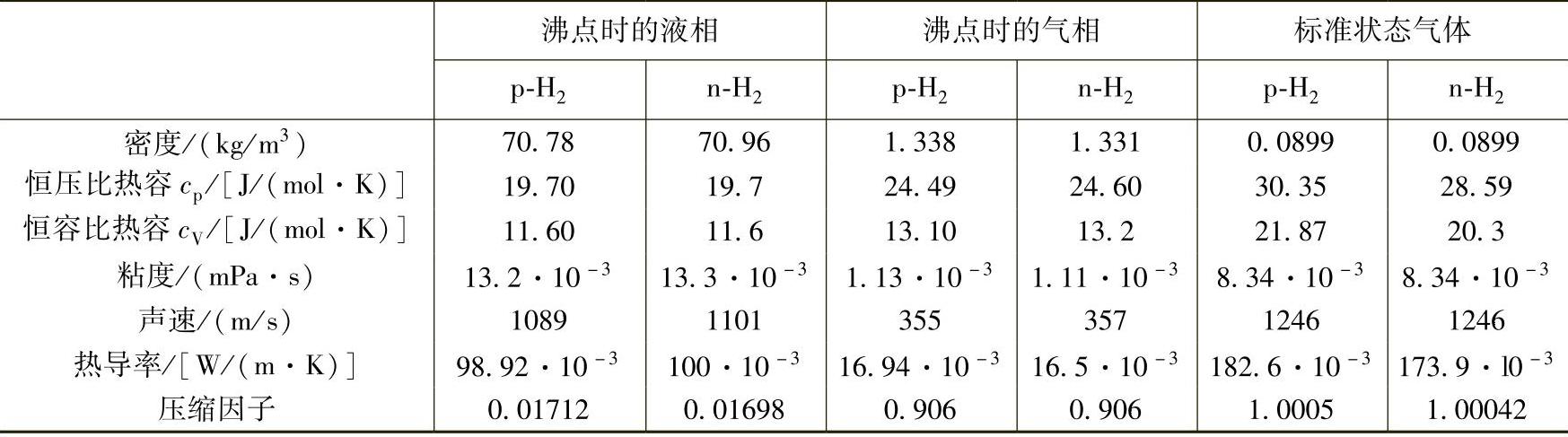
注：p-H₂为仲氢，n-H₂为正常氢（正氢和仲氢混合物），标准状态为0℃，1bar^[3]。

（1）氢气的气体状态方程

在低压状态下，H₂可以认为是理想气体，遵守理想气体定律：

式中，p为气体压力；V_m为1mol H₂的体积；R为气体常数，R=8.314J/（mol·K）；T是温度（K）。

在压力较高时，H₂的状态通常用van der Waals方程描述：

式中，a为反映气体分子之间的相互作用的参数；b为反映气体分子本身所占的体积的参数。

对于H₂，参数a=2. 476×10^-2m⁶Pa/mol²，b=2.661×10^-5m³/mol。

对H₂状态更精确的描述由下面的状态方程给出^[2]：

式中，a（p）和b（p）均是压力p的函数，分别由下面的式子给出：

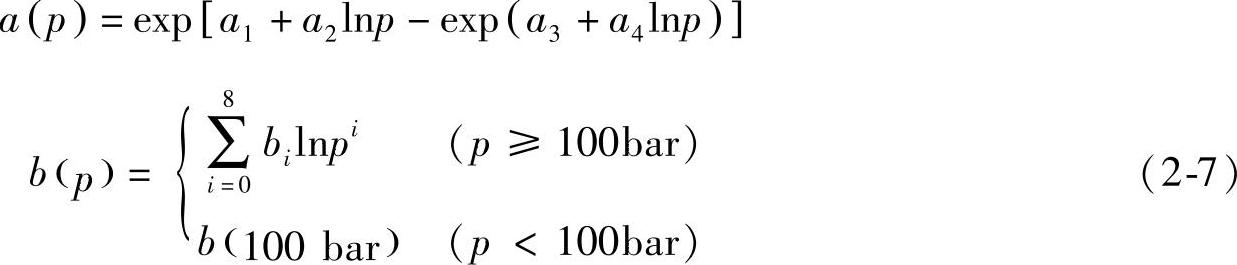
指数参数β对温度存在着微弱的依赖性，由下面的式子给出：

对于H₂，上述参数的取值列于表2-5中。

表2-5 氢气气体状态方程的参数^[2]

(www.daowen.com)

考虑到气体的非理性行为，在计算气体的热力学性质时应用逸度（fugacity）代替压力，逸度系数ϕ=f/p由下式定义：

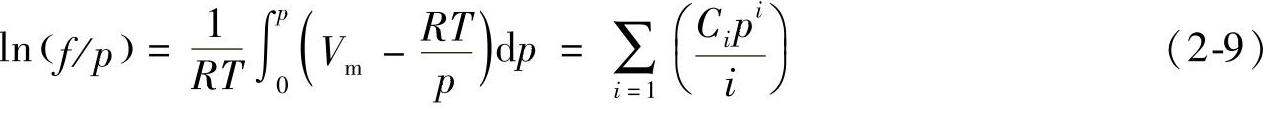
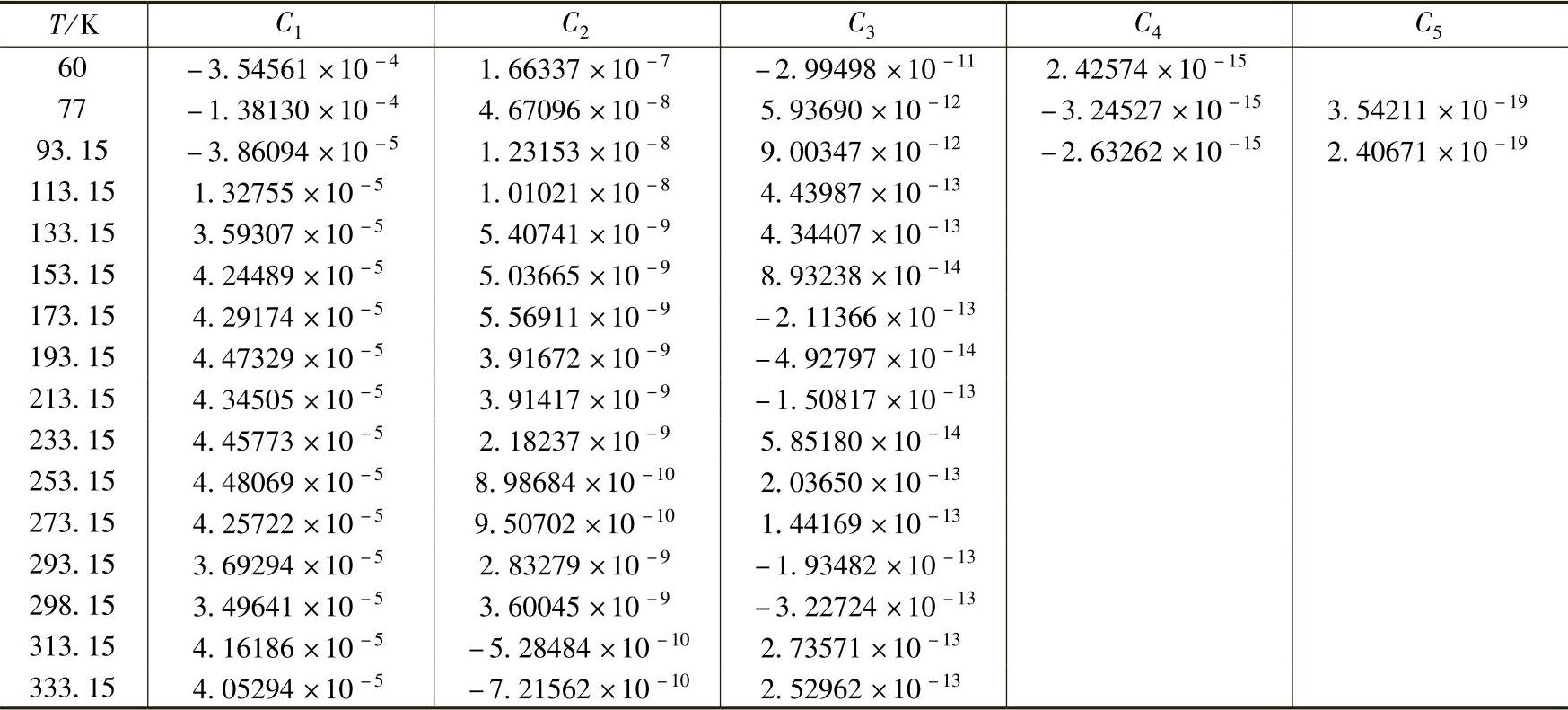
逸度系数表征了在一定压力下实际气体体积与理想体积的偏离，可以通过维里（Virial）系数C_i计算得到，相应的维里系数列于表2-6中^[3]。

表2-6 不同温度下氢气的维里系数^[3]

此时气体的化学势可以由下面的式子给出

对理想气体的偏离程度可以用压缩因子Z表示，其定义为

压缩因子与逸度系数之间的关系为

氢气的热力学性质与温度和压力有关，可以通过下面的方法计算：

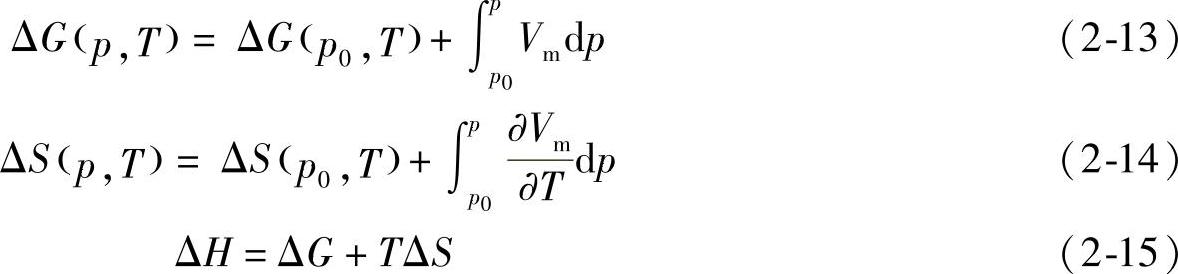
H₂的热力学函数随温度和压力变化的情况列于表2-7和表2-8中。对氢气的热力学性质更详细的描述可以参见综述^[4]。

表2-7 氢气热力学函数随温度的变化（1 bar）^[2]

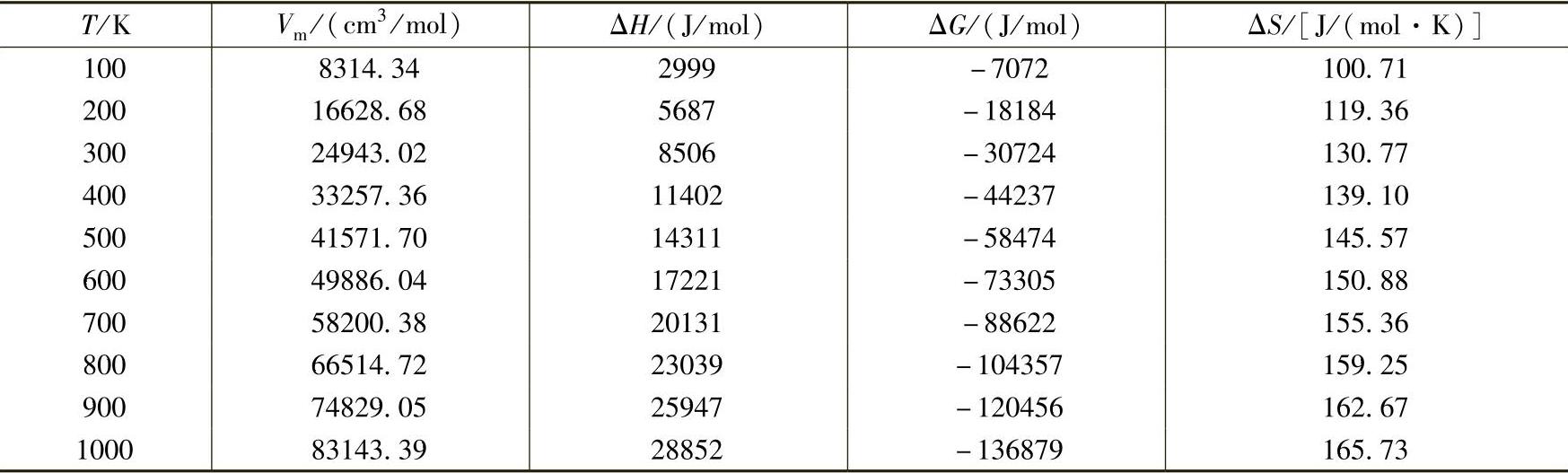
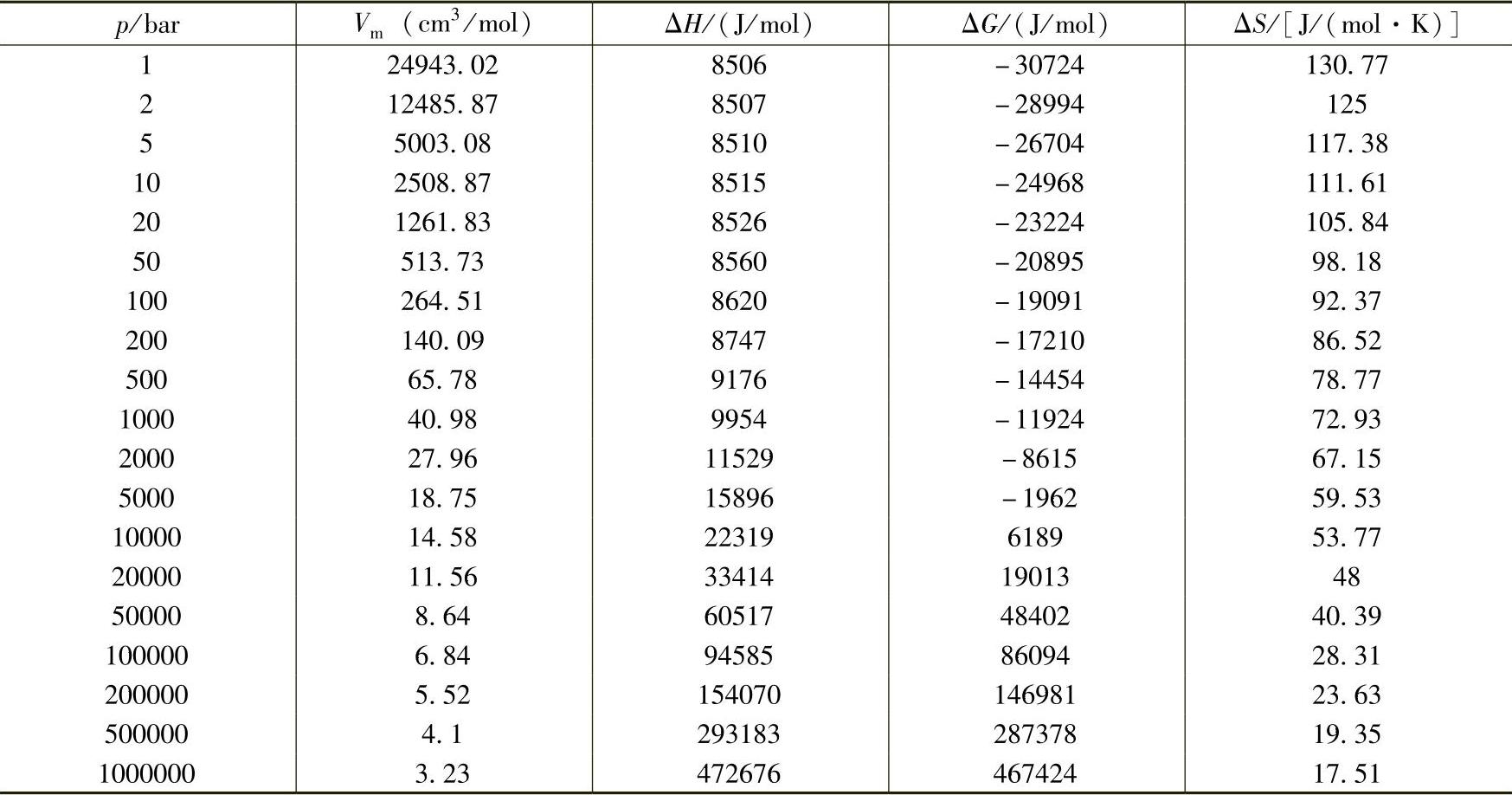
表2-8 氢气热力学函数随压力的变化（300K）^[5]

（2）液态和固态氢、金属氢

氢的相图如图2-4所示，其临界点和三相点总结于表2-9中。

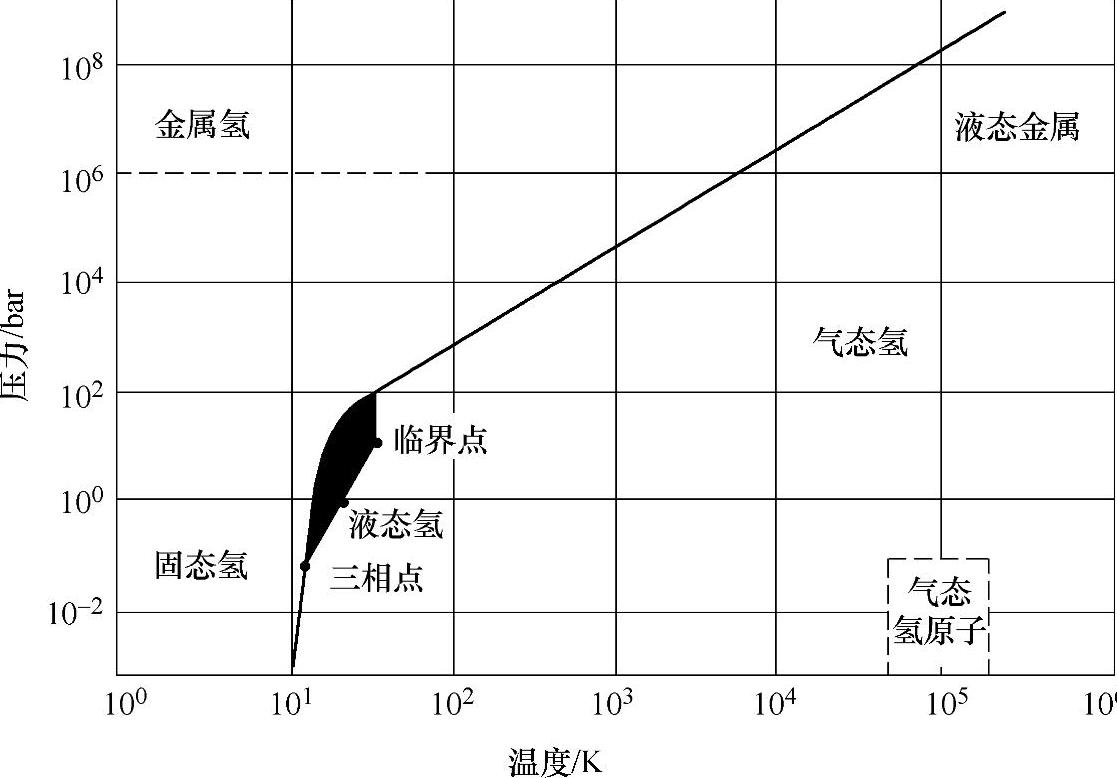
图2-4 H₂的相图^[6]

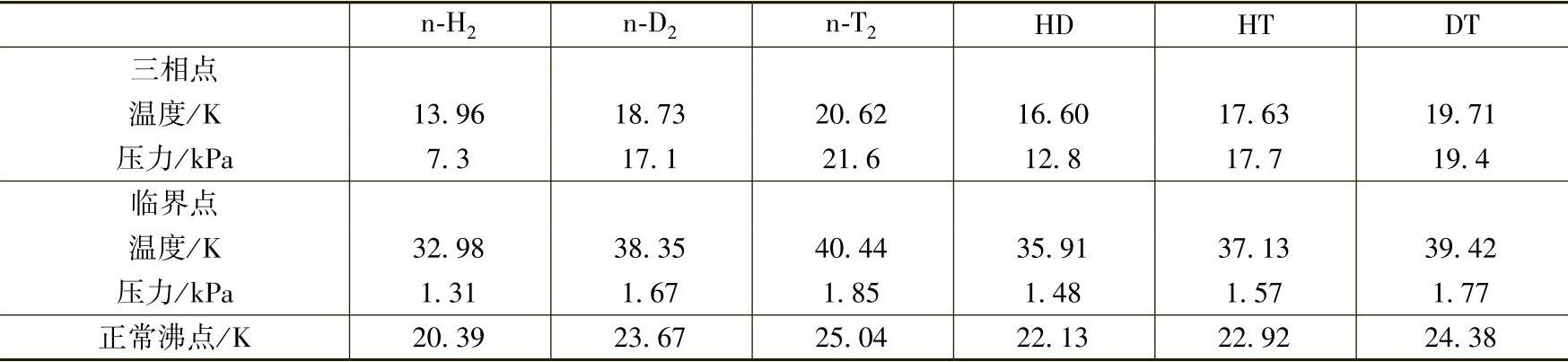
表2-9 几种氢同位素双原子分子的三相点和临界点

液态氢于1898年首次由James Dewar通过膨胀冷却法和他自己发明的Dewar瓶制备得到，次年他又获得了固态的氢。若需要使H₂保持液态不沸腾，需在20K以下通过加压获得。在液态氢中核自旋为0的仲氢占了绝大多数（99.79%）。氢的熔化曲线可以用下面的方程表示^[7]：

P_m=-51.49+0.1702(T_m+9.689)^1.8077 （2-16）

液态氢常用作高密度氢气存储介质，主要用于火箭推进器燃料，虽然其质量能量密度很高，但是其体积能量密度却低于绝大多数燃料。液态氢需要在低温下贮藏，低温系统的故障将导致H₂的泄漏，因此在液态H₂的存储和运输过程中需十分小心。

氢气固化时形成六方结构晶体，此时绝大多数分子是仲氢，固态仲氢的晶格参数为：a=376pm，c/a=1.623。六方结构的固态氢随着压力不同呈现出3种不同的物相。在较低压力下（0～110GPa），H₂分子质心呈六方密堆积排列，但是分子取向是随机的，统计上呈现P63/m的空间群，称为相I；当压力上升至110～150GPa时，在六方c轴上的分子取向是固定的，而在（0001）面上的分子取向仍然具有随机性，在a轴方向呈现一种非共度结构，称为对称性破坏的相（Broken Symmetry Phase，BSP）或相Ⅱ；当压力升到150GPa以上时，所有分子的取向都被固定，晶体结构为Cmc2_l，称为相Ⅲ^[8]。三种六方相的晶体结构如图2-5所示，其相变行为可以通过晶格振动谱的方法来研究，在Ⅰ-Ⅱ的相变中红外和Raman谱峰的变化是连续的，而在Ⅱ-Ⅲ的相变中，谱峰位置的变化出现突跃。如图2-6所示，在更低的温度下分子的旋转自由度被抑制而发生相变，形成面心立方结构Pa3，其结构如图2-5d所示。六方向立方相转化的温度在3K以下，随着其中正氢o-H₂比例的上升而线性上升^[9]。

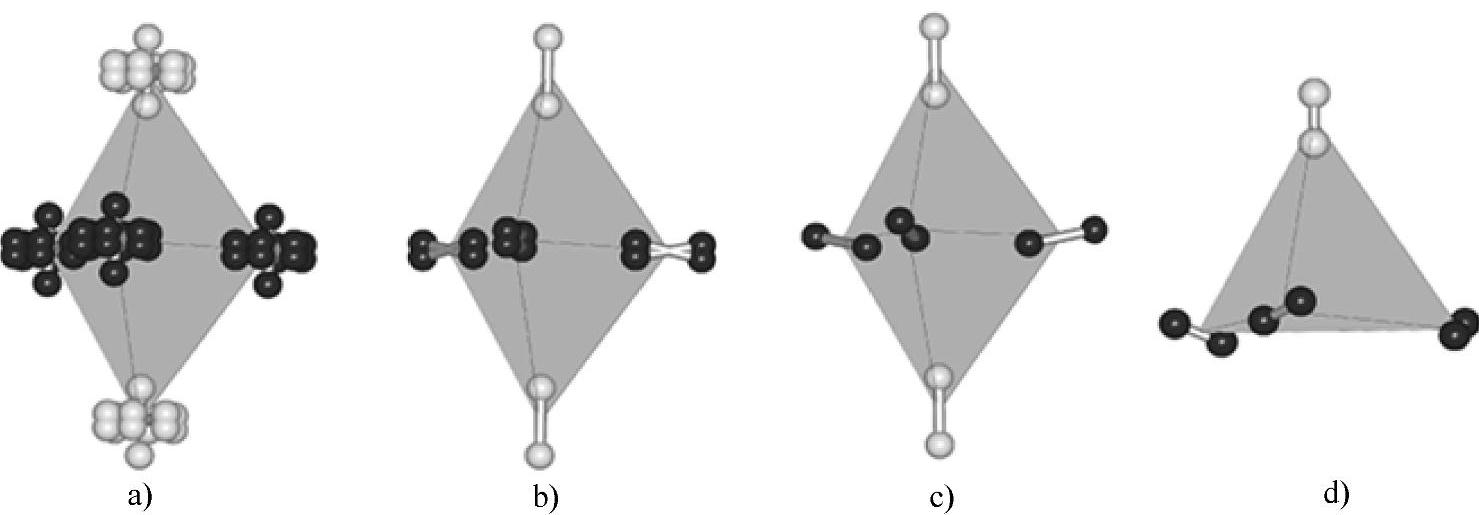
图2-5 三种六方相和立方相固态氢的结构示意图

a）六方相Ⅰ b）六方相Ⅱ c）六方相Ⅲ d）立方相

注：浅色分子位于六方的c轴或立方的[111]轴，结构的主要差异在于分子取向^[10]

无论是气态、液态还是固态，氢都是绝缘体。但在元素周期表中氢与碱金属位于同一族，因此很早就有关于是否存在金属态的氢的疑问。1935年物理学家预测在约25 GPa的超高压下，氢有可能体现出金属性^[11]。天文物理学家也认为在一些质量很大的行星（如木星、土星）核内由于其很高的压力也可能存在金属态的氢。理论预计金属态的氢将呈现出许多独特的物理学行为，包括在室温附近的超导特性^[12]以及可能存在的一种全新的量子有序结构。但同时实验上获得金属态的氢是极其困难的，最开始预测的25GPa压力明显偏低，Narayana等人利用金刚石对顶砧产生了327GPa的高压，但是固体氢仍然表现出光学透明的绝缘体态（见图2-7）^[13]。当前技术上已经能实现超过地心压力的约500GPa的超高压，尽管有一些研究者声称在实验中观察到了金属态的氢，但是仍然没有被公认的金属氢存在的实验证据。因此金属氢认为是高压物理学界的圣杯。对金属氢的实验研究在2008年取得了比较大的进展，利用脉冲激光加热高压下的氢发现了此前理论预测的熔点曲线的最大值^[14]，同时在高压下氢与硅的合金中发现了超导现象^[15]。

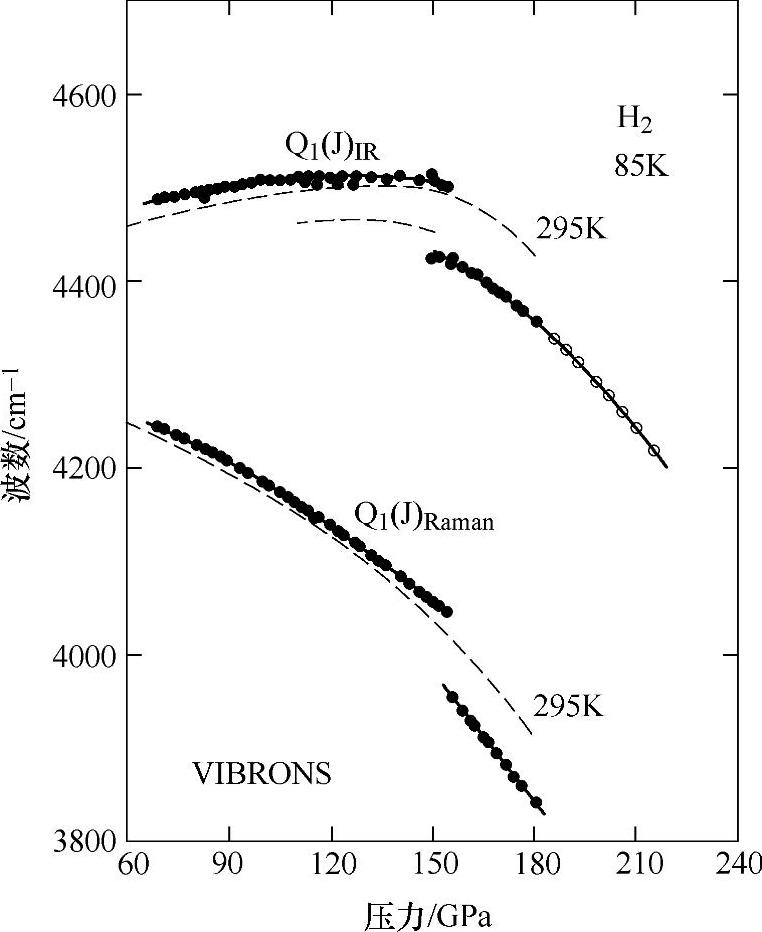
图2-6 随压力变化的H₂的红外（IR）和Raman振动谱峰的移动（在150GPa处的突变表明了Ⅱ-Ⅲ的相变，六方相Ⅰ的结果在图中用虚线表示^[8]）

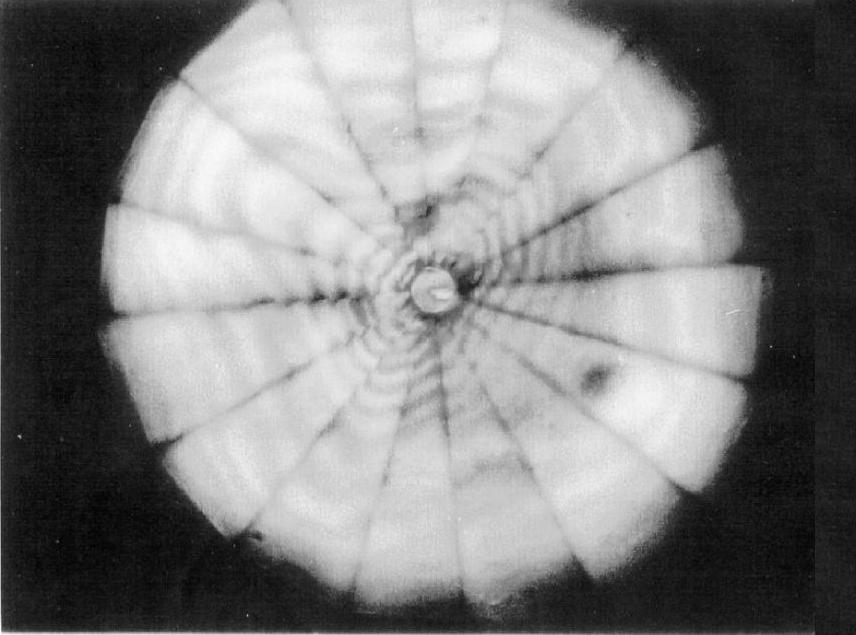
图2-7327 GPa下固体氢的透射和反射光照片（仍然呈现光学透明的状态，表明并未出现金属态的氢^[13]）