为研究两种不同的药物的抗癌疗效，采用老鼠进行试验，试验数据存放在“SurvivedRats.dat”数据文件中。实验过程为将实验老鼠接触致癌物质二甲基苯并蒽（DMBA）后，采用两种不同的药物分两组进行治疗，观察和记录2组实验老鼠在60h内的生存状态。第一组采用药物1（Drug 1）治疗，在30h时，出现第一只老鼠死亡（非癌症死亡），60h实验完成时有15只实验老鼠存活。第二组采用药物2（Drug 2）治疗，在14h、15h和25h时，分别有一只老鼠出现死亡（非癌症死亡），60h实验完成时也有15只实验老鼠存活。存活状态（Status）用数字表示，“0”为非癌症死亡、“1”为癌症死亡和“2”为存活。试采用计算存活率的经典模型Kaplan-Meier模型进行分析并给出解释。用Kaplan-Meier模型分析存活率的方法如下：

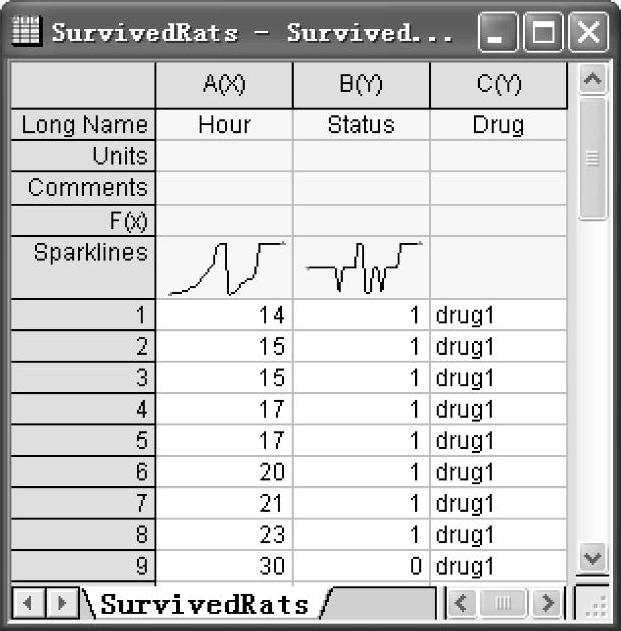
图12-74 “SurvivedRats.dat”工作表

（1）导入“Origin9.1\Samples\Statistics\Sur-vivedRats.dat”数据文件，其工作表如图12-74所示。工作表A（X）列为存活时间，B（Y）列为存活状态，C（Y）列为药物组列。

（2）选择菜单命令【Statistics】→【Survival Analysis】→【Kaplan-Meier Estimator...】，打开【Statistics/Survival Analysis：kaplanmeier】对话框进行设置。

图12-74“SurvivedRats.dat”工作表

（3）在“Input”栏中的“Time Range”“Censor Range”和“Grouping Range”分别选择工作表中的A（X）列、B（Y）列和C（Y）列。在“Censoring Value（s）”中选择“0”和“2”，在“Survival Table”栏中选中所有的复选框，在“Survival Plot”栏中选中“Survival”“Add confidence intervals”“One Minus Survival”和“Hazard”复选框，在“Test Equality of SA Functions”栏中选中所有的复选框。设置好的【Statistics/Survival Analysis：kaplanmeier】对话框如图12-75所示。(www.daowen.com)

（4）单击“OK”按钮，完成存活率计算，数据和图表（略）保存在自动生成的存活率报告工作表中。

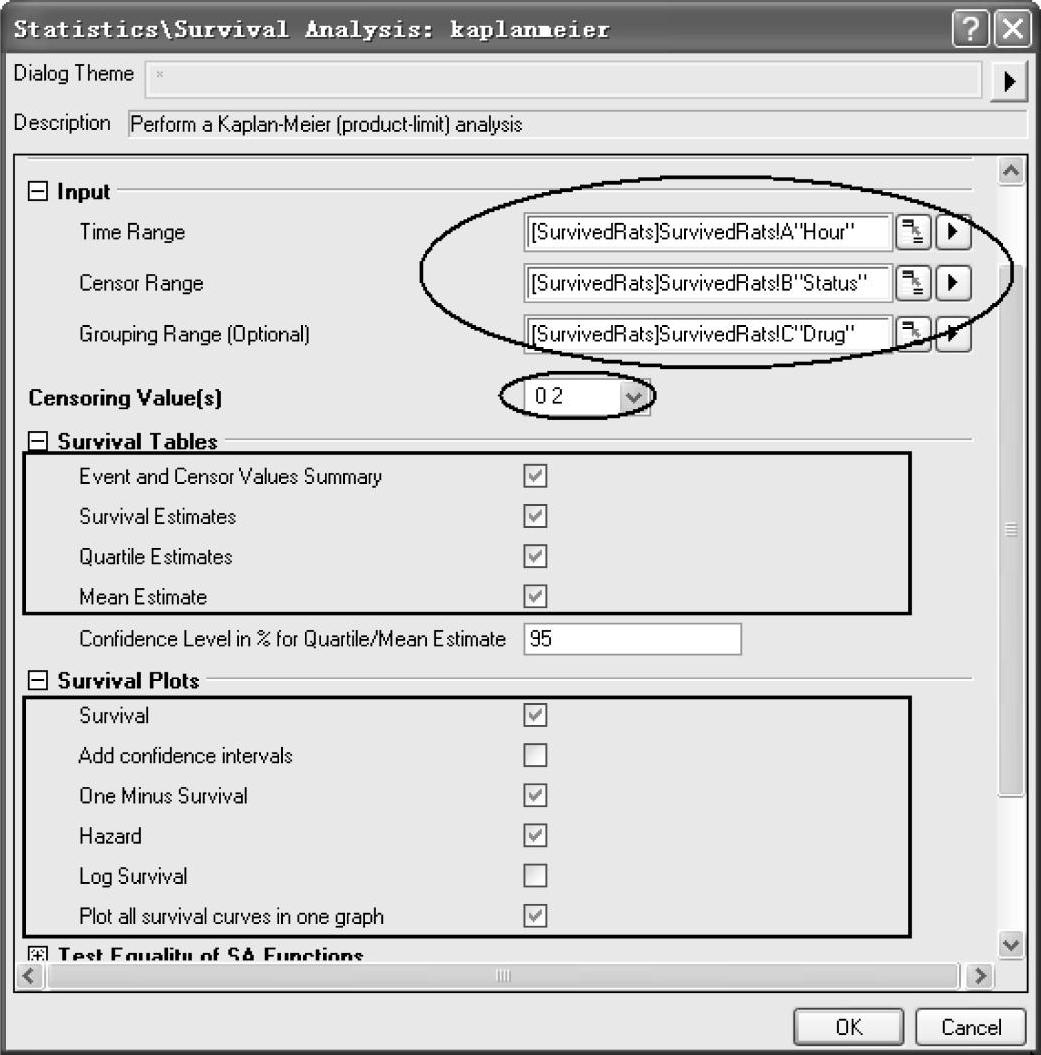
图12-75 设置好的【Statistics/Survival Analysis：kaplanmeier】对话框

分别双击存活率报告工作表中的存活率图（Survival Plots）图例，得到存活率函数图（Survival Function）和风险函数图（Hazard Function），分别如图12-76a和图12-76b所示。存活率函数图图中曲线下降越快，则存活率越低。可以看到药物1（Drug 1）一直比药物2（Drug2）下降的速率快，因此可以认为药物2的抗癌效果比药物1好。风险函数图图中曲线上升越快，则风险越大。可以看到药物1（Drug 1）一直比药物2（Drug2）上升速率快，因此可以认为药物2的抗癌可靠性比药物1好。

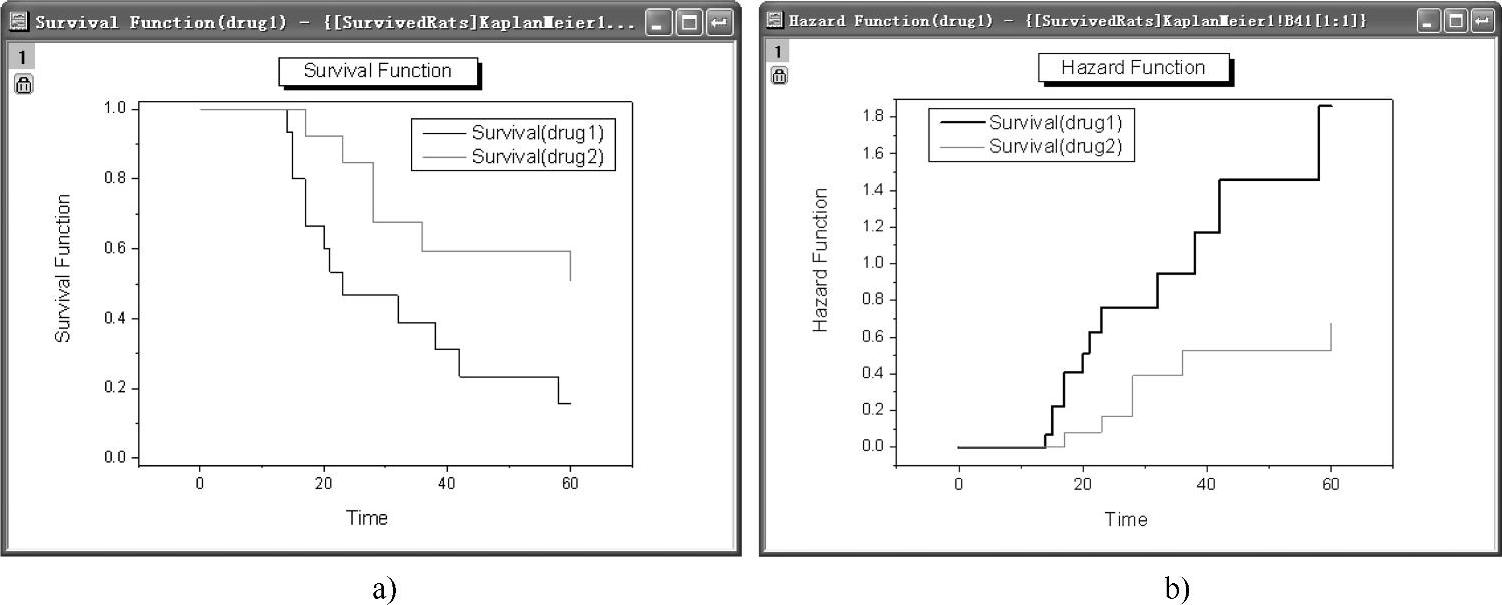
图12-76 存活率函数图和风险函数图