单因素重测方差分析（One-way repeated measures ANOVA）是专业版OriginPro9.1的功能，它主要用于独立变量的重复测量。在重复测量的情况下，采用单因素方差的无关性假设则不可行，这是因为可能存在重复的因素在某一水平上相关。

与单因素方差分析一样，单因素重测方差分析可用于检验不同测量的均值和不同主题的均值是否相等。除确定均值间是否存在差别外，单因素重测方差检验还提供了多均值比较，以确定哪一个均值有差别。单因素重测方差检验对数据的要求是：每一水平数据样本大小相同，可采用索引存放格式数据和原始存放格式数据。下面结合实例，对索引存放格式数据进行单因素重测方差分析。

（1）导入“Origin 9.1\Samples\Statistics\ANOVA\One-Way_RM_ANOVA_indexed.dat”数据文件，如图12-58所示。该工作表记录了3种不同剂量的药物对30组样本的影响试验数据，试分析不同剂量是否对样本有不同的影响。

（2）选择菜单命令【Statistics】→【ANOVA】→【One-Way Repeated Measures ANOVA】，在弹出的【ANOVAOneWayRM】对话框中设置参数。在“Input Data”列表框中选择“indexed”；在“Factor”“Data”和“Subject”中分别选择工作表中的B（Y）列、C（Y）列和A（X）列。选中“Means Comparison”中的“Bonferroni”复选框进行均值比较。在“Plots”栏中选中“Means Plot[SE as Error]”和“Means Compari-son Plot”复选框。设置好的【ANOVAOneWayRM】对话框如图12-59所示。

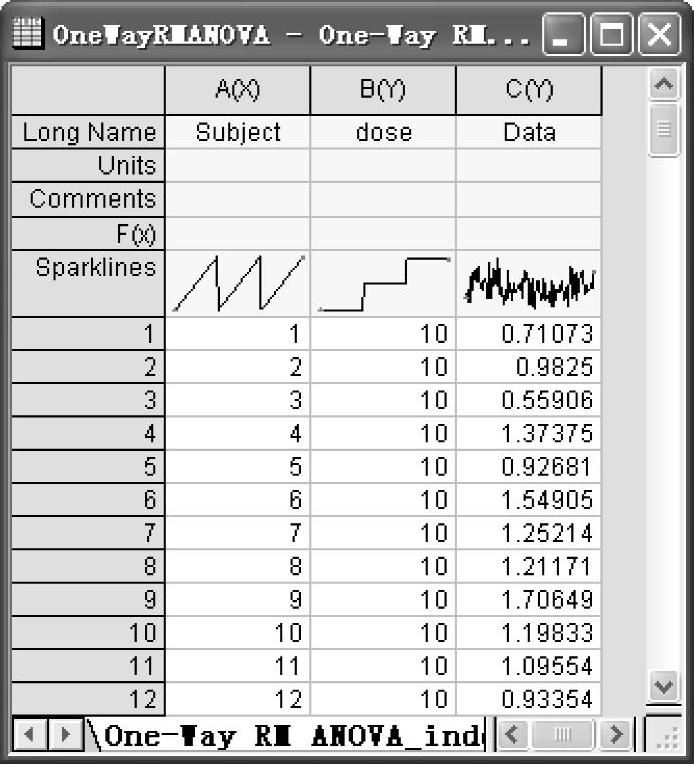
图12-58 “One-Way_RM_ANOVA_indexed.dat”工作表

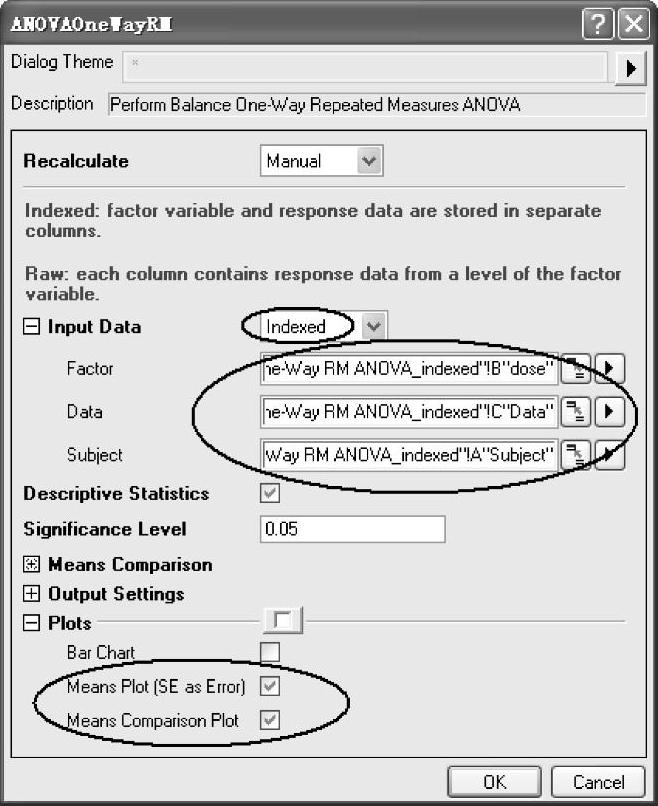
图12-59 设置好的【ANOVAOneWayRM】对话框(www.daowen.com)

（3）单击“OK”按钮，创建单因素重测方差分析报告，如图12-60所示。

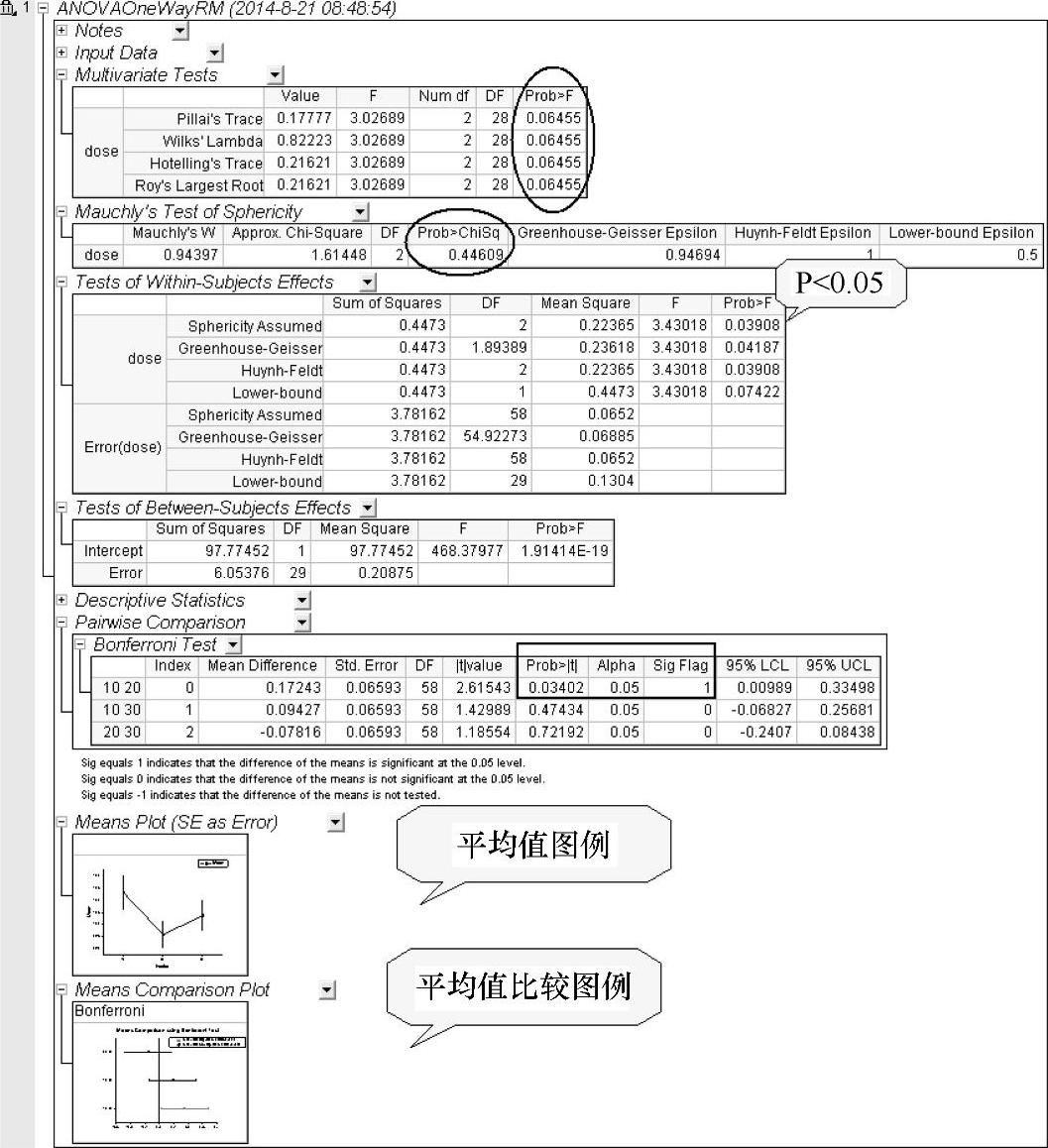
图12-60 创建的单因素重测方差分析报告

在该单因素多重方差分析报告中，多重分析表（Multivariate Tests）中4种分析的P值均为0.06455，可认为在该3种水平测试条件下的平均值没有显著差别。Mauchly′s分析表（Mauchly′s Test of Sphericity）中的显著性水平（0.44609）大于0.05，可认为Sphericity假设成立。组间影响表（Test of Between-Subjects Effects）中的Sphericity假设条件下，P值为0.03908<0.05。因此，可得出结论，从统计意义上讲，采用Sphericity假设的单因素多重方差分析，该3种水平测试条件下的平均值是不同的，即剂量是一个显著的影响因素。配对比较（Pairwise Comparison）表中采用Bonferroni测试能有效进一步分析具体是哪一种水平的均值是不同的。表中P=0.03402<0.05和Sig Flag=1，表明剂量1（dose1）和剂量2（dose2）的均值显著不同。双击平均值图（Means Plot）和均值比较图（Means Comparison Plot）图例，在打开的平均值图（图12-61a）和均值比较图（图12-61b）中可进一步证明上述结论。

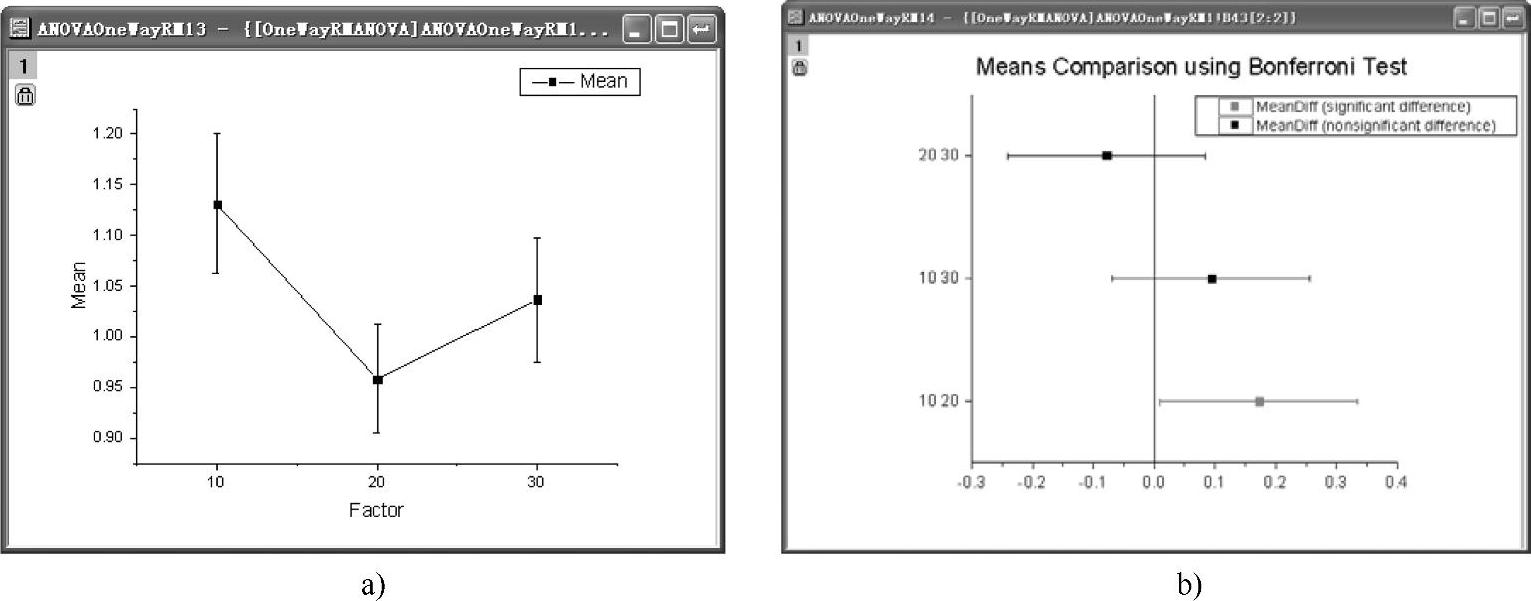
图12-61 平均值图和均值比较图