在实际测量条件下，多次测量同一物理量的过程中，误差的正负号和绝对值的变化时大时小、时正时负，这种以不可预知的方式变化的误差称为随机误差。随机误差产生的原因很多，一般可分为两大类：

第一类，实验中各种微小因素的变动，如实验装置在各次调整操作上的变动性、气流的扰动、温度的起伏、电压的波动、杂散电磁场的干扰等引入的误差；

第二类，观察者在对准目标、确定平衡、估读数据时以及其分辨能力所限所引入的误差。

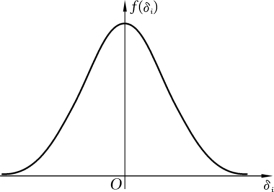
图1-2-1　正态分布曲线

单就每一次测量而言，随机误差的出现是没有规律的，大小和方向都是不可预知的。但只要进行足够多次的测量，就会发现随机误差服从一定的统计规律。根据随机误差的性质，有多种处理随机误差的理论和方法。最常见的所谓遵从正态分布（又称高斯分布，此时只考虑随机误差）的误差如图1-2-1所示。图1-2-1中，横坐标δi＝Δxi＝xi－A，表示误差，纵坐标f（δi）表示与误差出现的概率有关的概率密度函数。由图1-2-1可知，遵从正态分布的随机误差有以下几点特征。

（1）单峰性：绝对值小的误差比绝对值大的误差出现的概率大。

（2）对称性：绝对值相等的正负误差出现的概率相等。

（3）有界性：在一定的条件下，误差的绝对值不会超过一定的范围。

（4）抵偿性：在测量次数n→∞时，全部误差的代数和等于零，即

(www.daowen.com)

根据概率论的数学方法可以导出

式中：σ是一个与实验条件有关的常数，称为标准偏差，其值为

式中：n为测量次数，各次测量的随机误差为δi（i＝1，2，…，n）。

随机误差的正态分布曲线的形状与σ值有关。σ值越小，分布曲线越尖锐，峰值f（δi）越高，说明绝对值小的误差占多数，且测量值的离散性较小、重复性好，测量精密度较高；反之，σ值越大，分布曲线越平坦，则测量值的离散性较大，测量精密度较低。

对任意一次测量，其测量值误差出现在区间（－σ，＋σ）的概率为

用同样的方法可算得，误差出现在区间（－2σ，＋2σ）的概率为95.5%，出现在区间（－3σ，＋3σ）的概率为99.7%。测量误差的绝对值大于3σ的概率仅为0.3%，因此在有限次的测量中，误差超出区间（－3σ，＋3σ）的情况几乎不会出现，所以把3σ称为极限误差。