用拉氏变换求解线性电路的时域响应时，需要把求得的响应的拉氏变换式反变换为时间函数.由象函数求原函数的方法有：

(1)利用公式

(2)对简单形式的F(s)可以查拉氏变换表得原函数.

(3)部分分式展开法.

下面主要介绍部分分式展开法(也称海维赛展开法).

设象函数的一般形式为

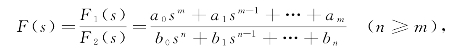
即F(s)为真分式(如果不是真分式，需要先化为真分式，对真分式使用海维赛展开法).

下面讨论分母F2(s)=0对应根的情形.

①不同单根的情形

若F2(s)=0对应n个不同的单根p1，p2，…，pn(或写成s1，s2，…，sn)，则可将F(s)分解为部分分式之和，过程为

其中，待定常数的确定有如下方法：

方法一，按

(www.daowen.com)

来确定.

方法二，用求极限方法(最后用洛必达法则转化为求导)确定ai的值.

ai=

总结上述，得到由F(s)求f(t)的步骤：

(1)n=m时将F(s)化成真分式和多项式之和；

(2)求真分式分母的根，确定根的情形；

(3)将真分式展开成部分分式，求各部分分式的系数；

(4)对每个部分分式和多项式逐项求拉氏反变换.

例1 已知F(s)=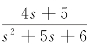，求原函数f(t).

关于拉氏反变换求解也可以使用留数法，留数法的优势是不用作反变换就可以求出f(t)，并可用于无理分式，编者总结了海维赛部分分式展开法和留数法公式如表9-3所示.

表9-3 拉氏反变换求解方法及公式

注：极点是使象函数F(s)对应的真分式的分母为0(使真分式趋于无穷大)的点，与之相关的概念还有“零点”，零点是指使F(s)对应的真分式的分子为0(使真分式为0)的点.