1.三角级数

在自然科学和工程技术中，对周期现象的数学描述就是周期函数.简单的周期现象，如单摆的摆动、音叉的振动等都可用正弦函数y=A sin(ωx+φ)来描述，但是复杂的周期函数，如电子技术中常用到的周期为T的矩形波、开关元件的频率性态或脉冲的传输问题等就不是正弦周期函数.

结合上节介绍过的用幂级数展开式表示函数和讨论函数的方法，我们也想将复杂的周期函数表示为无限多个正弦函数与余弦函数之和.

三角函数系及正交性：由1，cosx，sinx，cos2x，sin2x，…，cosnx，sinnx，…组成的函数序列叫三角函数系.三角函数系具有如下性质：如果k与n是非负整数，有

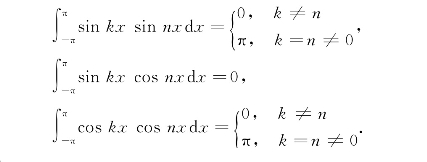
即三角函数系中任何不同的两个函数的乘积在[-π，π]上的定积分为0，这种性质称为三角函数系的正交性.

级数的各项均由三角函数系中的函数构成的函数项级数

或简写为

其中，a0，an，bn(n=1，2，…)是常数，则式(8-9)称为三角级数.

2.周期为2π的函数的傅立叶级数

引进傅立叶级数(部分电子通信类教材中也称“傅里叶级数”)的基本思想是用三角级数表示一般的周期函数.下面讨论如何把周期为2π的函数展开成三角级数.这里须解决两个问题：

(1)什么条件下函数f(x)能表示为三角级数?

(2)如果f(x)可以表示为三角级数，又如何确定常数a0，a1，b1，…?

假设f(x)在区间[-π，π]上能展开形成三角级数(8-9)，即

那么级数(8-10)的系数a0，an，bn(n=1，2…)与函数f(x)有什么关系呢?

对式(8-10)在区间[-π，π]上进行积分

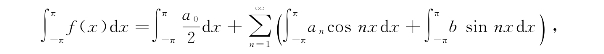
根据三角函数系的正交性，有

即

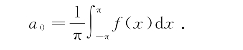
其次，求an：

虽然我们从形式上作出了函数f(x)的傅立叶级数(8-11)，但函数f(x)的傅立叶级数(8-11)是否在[-π，π]上收敛?如果收敛是否一定收敛于函数f(x)呢?一般说来，答案不是肯定的，那么f(x)究竟满足什么条件可以展开成傅立叶级数?下面直接给出一个收敛定理，不加证明.

收敛定理 (狄利克雷(Dirichlet)充分条件)设f(x)是周期为2π的周期函数，如果它满足：

(1)在一个周期内连续或只有有限个第一类间断点；

(2)在一个周期内至多只有有限个极值点.则f(x)的傅立叶级数收敛，并且

当x是f(x)的连续点时，级数收敛于f(x)；

当x是f(x)的间断点时，级数收敛于[f(x-0)+f(x+0)].

收敛性定理说明：只要函数在[-π，π]上至多有有限个第一类间断点，并且不作无限次振动，那么函数的傅立叶级数在连续点处收敛于该点的函数值，在间断点处收敛于该点的左极限与右极限的算术平均值.由此可见，函数能展开成傅立叶级数的条件比较低.

例1 设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为将f(x)展开成傅立叶级数.

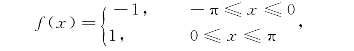
解 所给函数满足收敛定理的条件，如图8-1所示，它在x=kx(k=0，±1，±2，…)处不连续，在其他点处连续，从而由收敛定理知f(x)的傅立叶级数收敛，并且当x=kπ时级数收敛于

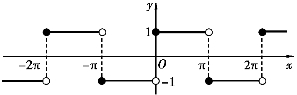
图8-1

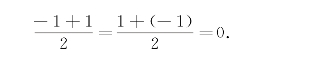
3.正弦级数和余弦级数(www.daowen.com)

定理 设f(x)是周期为2π的函数，在[-π，π]上可积，则(1)当f(x)为奇函数时，它的傅立叶系数为

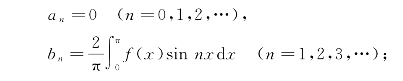
(2)当f(x)为偶函数时，它的傅立叶系数为

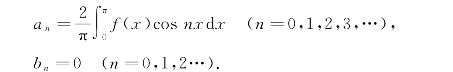
上述结论利用定积分的计算容易得到，不给予证明.

这个定理说明：如果f(x)为奇函数，那么它的傅立叶级数是只含有正弦项的级数

称为正弦级数.

如果f(x)为偶函数，那么它的傅立叶级数是只含有常数项和余弦项的级数

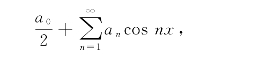
称为余弦函数.

例3 将函数展开成傅立叶级数.

解 所给函数在[-π，π]满足收敛定理的条件，并且在每一点x处都连续，由于f(x)是偶函数，故bn=0(n=1，2，…).

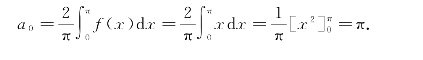
4.在[0，π]上的傅立叶级数

定义 如果f(x)为定义在[0，π]上的函数，可以在[-π，0]上补充函数的定义，得到一个定义在[-π，π]上的函数F(x)，使F(x)在[-π，π]上成为奇函数(偶函数)，且满足收敛定理的条件.按这种方式补充定义，拓广函数的定义域的过程称为延拓.如果构造F(x)成为[-π，π]上的奇函数，则称此延拓为奇延拓；如果构造F(x)成为[-π，π]上的偶函数，则称此延拓为偶延拓.

例4 将f(x)=x(0≤x≤π)分别展开为正弦级数和余弦级数.

当x=0时，上述余弦级数收敛于

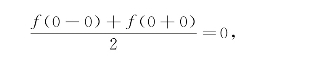
当x=π时，上述余弦级数收敛于

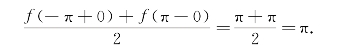
5.以2l为周期的周期函数的傅立叶级数

前面我们讨论了以2π为周期的周期函数的傅立叶级数展开式.那么，如何将周期为2l的周期函数展开为傅立叶级数?这个问题，结合前面讨论的周期为2π的函数的傅立叶级数的结果，通过变量代换方法可以解决，下面直接给出定理.

定理 设周期为2l的周期函数f(x)满足收敛定理的条件，则它的傅立叶级数展开式为

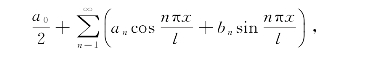
其中系数an，bn为

此级数收敛，并且有

习题8-5

1.把下列周期为2π的函数展开成傅立叶级数.

(1)f(x)=2x2 (-π≤x≤π)；

(2)f(x)=x (-π＜x≤π)；

2.将函数f(x)=2x2(0≤x≤π)展开成为正弦级数.

3.将函数f(x)=|x|(-1≤x≤1)展开成傅立叶级数.