函数项级数中简单而常见的一类级数就是各项都是幂函数的函数项级数，即幂级数.它的形式是

a0+a1x+a2x2+…+anxn+…，

(8-5)

记为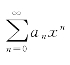，其中a0，a1，…，an，…称为幂级数的系数.例如都是幂级数.

幂级数更一般的形式为

a0+a1(x-x0)+a2(x-x0)2+…+an(x-x0)n+….

上式显然可以通过变量代换t=x-x0的方法化为(8-5)形式，所以只需讨论幂级数(8-5)就行了.

对于一个给定的幂级数，x取哪些值时收敛，取哪些值时发散呢?怎样求幂级数的收敛域和发散域呢?(www.daowen.com)

定理1 如果幂级数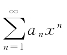不是仅在一点x=0处收敛，也不是在整个数轴上都收敛，则必有一个完全确定的正数R，使得：

当|x|＜R时，幂级数绝对收敛；

当|x|＞R时，幂级数发散；

当x=R与x=-R时，幂级数可能收敛也可能发散.

正数R通常叫幂级数(8-5)的收敛半径.根据幂级数在x=±R处的收敛性可以确定它在区间(-R，R)，[-R，R)，(-R，R]或[-R，R]上的收敛性，这个区间称为幂级数(8-5)的收敛区间.

定理2 对于幂级数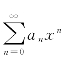(an≠0，n=0，1，2，…)，如果，其中an，an+1是幂级数的相邻两项的系数，那么这个幂级数的收敛半径是

解 级数缺少奇次幂的项，定理2不能直接应用，应用比值审敛法求收敛半径