一般来说，用二重积分的定义来计算二重积分是很困难的，下面我们在直角坐标系中把二重积分化为累次积分来计算.

当f(x，y)≥0时，由二重积分的几何意义有V=(x，y)dσ.

如图7-9，设积分区域D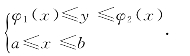

下面用定积分中求平行截面的面积为已知的立体体积的方法，来计算V的值.在[a，b]上任一点x处用垂直于x轴的平面去截曲顶柱体，得到一个以区间[φ1(x)，φ2(x)]为底，曲线z=f(x，y)(x固定，z是y的函数)为曲边的曲边梯形(如图7-10)，面积为

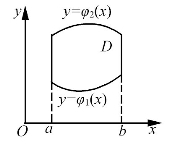
图7-9

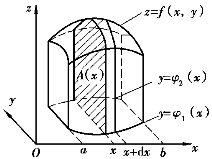
图7-10

从而得到曲顶柱体的体积为

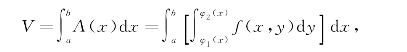
即

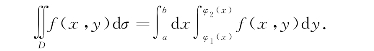
由此可见，二重积分的计算可以化为两次定积分的计算，这种方法称为累次积分法.

以上讨论中假定f(x，y)≥0，在一般情况下，结论同样成立.

类似地，如果积分区域D可用不等式组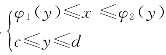表示(如图7-11)，其中φ1(y)和φ2(y)在[c，d]上连续，则(x，y)dx.

如果积分区域D不属于上述两种类型，这时，可以用平行于坐标轴的直线把D分成几个部分区域，D上的积分就化成每部分区域上的积分之和(如图7-12).

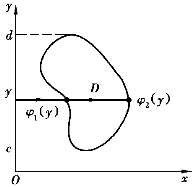
图7-11

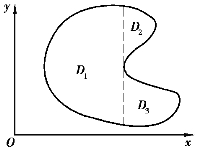
图7-12

例1 试将(x，y)dσ化为两种不同次序的累次积分，其中D是由y=x，y=2-x和x轴所围成的区域.

解 首先画出积分区域D，并求出边界曲线的交点(1，1)，(0，0)及(2，0)，如果先积y后积x(如图7-13)，将积分区域D投影到x轴上，则积分区域D分成两部分D1和D2，即(www.daowen.com)

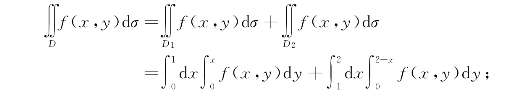
如果先积x后积y(如图7-14)，则将积分区域D投影到y轴上，即

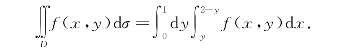
由此可见，恰当地选择积分次序，有时能使计算比较简便.

例2 计算xydσ，其中区域D是直线y=1，x=2，及y=x所围成的三角形区域.

解 首先画出积分区域D(如图7-15).

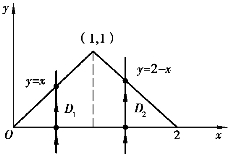
图7-13

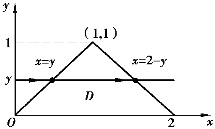
图7-14

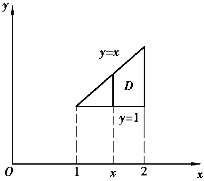
图7-15

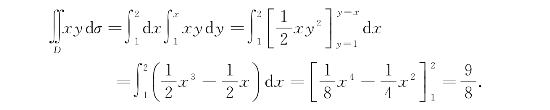
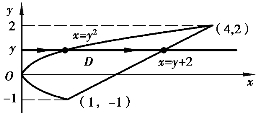
图7-16

例3 计算二重积分(x+y)dσ，其中D是由抛物线y2=x与直线y=x-2围成的区域.

解 首先画出积分区域D(如图7-16)，并求出边界曲线的交点(1，-1)，(4，2)，积分区域投影到y轴，有

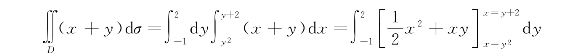
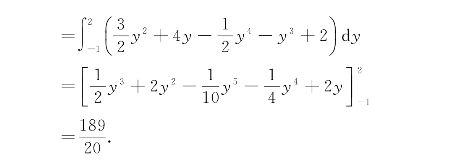
习题7-6